Реферат: Порівняння функцій та їх застосування

Якщо функція замінюється на де якому кроці через , то різницяь називається абсолютною похибкою, а відношення — відносною похибкою зробленої заміни. Якщо вивчається поведінка функції при то часто доцільно замінити її функцією такої, що 1) функція в певному значенні більш проста, ніж функція ; 2) абсолютна похибка прямує до нуля при

В цьому випадку говорять, що наближає функцію поблизу точки . Такою властивістю володіють наприклад, всі нескінченно малі при функції f і g. Нижче показано, що серед них лише ті, які еквівалентні між собою:

володіють тією властивістю, що не тільки абсолютна похибка , але і відносна прямує до нуля при

В цьому значенні функції, еквівалентні заданій, наближають її краще, ніж інші функції навіть того ж порядку, що і дана при

Наприклад, функції є нескінченно малими при так само як і а тому абсолютні похибки при заміні sin кожна з них прямує до нуля при

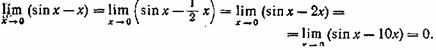
Але лише одна зі всіх перерахованих функцій, а саме: має ту властивість, що відносна похибка при заміні цією функцією прямуватиме до нуля при

Прямування відносної похибки до нуля при можна записати, використовуючи символ “o мале»:

Сформулюємо сказану характеристичну властивість еквівалентних функцій у вигляді теореми.

Теорема 1. Для того, щоб функції і були еквівалентними при необхідно і достатньо, щоб при виконувалася умова

(1.32)

Доведення необхідності. Нехай при тобто

де . Тоді

де при , тобто маємо (1.32).

Доведення достатності. Нехай виконується умова (1.32), тобто

де . Тоді

де при тобто при

Отже, ми показали, що функції і еквівалентні при тоді і тільки тоді, коли відносна похідна (або прямує до нуля при )

Наслідок. Нехай де с - стала. Тоді f~cg і g=cf+o(f) при

Доведення. Якщо , то , і значить при . Звідси, з теореми 1 маємо а значить (див. кінець п. 1.2) .

Теорема 2. Нехай ~ і ~ при Тоді якщо існує

(1.33)

то існує і , причому

(1.34)

Доведення. Умова при означає, що

де , а умова при -що , де . Крім того, оскільки існує границя (1.33), функція визначена в деякому проколеному околі точки і, отже, всюди в цьому околі виконується нерівність . Оскільки і, очевидно, в деякому проколеному околі точки , то і функція володіє тією ж властивістю. Тому функція визначена в деякому проколеному околі точки .