Реферат: Порівняння функцій та їх застосування

ЗМІСТ

Вступ 3

1. ПОРІВНЯННЯ ФУНКЦІЙ. ОБЧИСЛЕННЯ ГРАНИЦЬ 4

§1. ДЕЯКІ ЧУДОВІ ГРАНИЦІ 4

§2. ПОРІВНЯННЯ ФУНКЦІЙ 9

§3. ЕКВІВАЛЕНТНІ ФУНКЦІЇ 18

§4. МЕТОД ВИДІЛЕННЯ ГОЛОВНОЇ ЧАСТИНИ ФУНКЦІЇ І ЙОГО ЗАСТОСУВАННЯ ДО ОБЧИСЛЕННЯ ГРАНИЦЬ. 21

ВИСНОВОК 26

Вступ

Нехай дано множину Е дійсних чисел. Якщо кожному числу за певним законом поставлено у відповідність одне дійсне число y, то кажуть, що на множині Е задана (визначена) функція, і записують . При цьому x називають незалежною змінною, або аргументом, а y – залежною змінною, або функцією.

В цій роботі передбачається розглянути: О-символіку Ландау для функцій однієї змінної, заданої в проколотому околі довести ряд тверджень про арифметичні дії над О-символами та еквівалентними функціями; деякі важливі границі; способи порівняння функцій та ін.

Розглянути метод виділення головної частини функції в застосуванні до обчислення до границь. Теоретичні дослідження проілюструвати розв’язанням вправ

ПОРІВНЯННЯ ФУНКЦІЙ. ОБЧИСЛЕННЯ ГРАНИЦЬ

ДЕЯКІ ЧУДОВІ ГРАНИЦІ

В цьому пункті обчислюються границі, які неодноразово зустрічатимуться надалі.

Лема 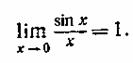1.

(1.1)

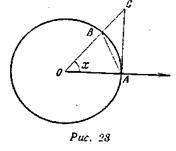
Доведення. Розглянемо круг радіусом R з центром в точці О. Нехай радіус 0В утворює кут , з радіусом ОА. З’єднаємо точки А і В відрізком і проведемо з точки А перпендикуляр до радіуса ОА до перетину в точці С з продовженням радіуса 0В (мал. 28). Тоді площа трикутника АОВ рівна , площа сектора AОB рівна а площа трикутника АОС рівна Трикутник АОВ є частиною сектора АОВ, який у свою чергу є частиною трикутника АОС; тому

звідки

отже,

або, замінюючи величини їм оберними

(1.2)

Зауважимо, що через парність функцій і нерівність (1.2) справедлива і при . Оскільки функція неперервна і , то з (1.2) при слідує рівність (1.1).

Наслідок 1.

(1.3)

Дійсно,

Наслідок 2.

(1.4)

Функція строго монотонна і неперервна на відрізку , тому обернена функція також строго монотонна і неперервна на відрізкуе . Оскільки , то записи і еквівалентні. Щоб обчислити границю (1.4), застосуємо правило заміни змінної для границю неперервних функцій. Поклавши , маємо

Наслідок 3.

(1.5)

Ця рівність випливає аналогічно попередній з (1.3).

Лема 2.

(1.6)

Рівність

(1.7)

де Звідси випливає, що для будь-якої послідовності натуральних чисел, такї, що

(1.8)

маємо

(1.9)

Дійсно, нехай задано ; з (1.7) випливає, що знайдеться таке що при

(1.10)

а з умови (1.8) випливає, що існує таке що при тому в силу (1.10)

при що і означає виконання рівності (1.9).

Нехай тепер послідовність така, що

тобто

(1.11)

Покажемо, що При цьому без обмеження спільності можна вважати, що Для довільного знайдеться таке натуральне що і, отже, причому в силу Тому маємо:

(1.12)

Наголошуючи, що в силу (1,9)

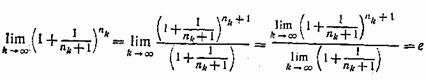
і

і переходячи до границю в нерівності (1.12) при , отримаємо

Оскільки —первісна послідовність, яка задовільняє умовам (1.11), то тим самим доведено, що

(1.13)

Нехай тепер послідовність така, що.

тобто,

(1.14)

Покладемо , тоді і при чому без обмеження спільності можна вважати, що Тоді

,

де

і

і через вже доведену рівність (1.13)

Але була довільною послідовністю, що задовольняє умовам (1.14), тому

(1.15)

Таким чином, функція має в точці О границі з ліва і права, рівні одному і тому ж числу е. Тому існує і її двостороння границя при , яка також рівна е.