Реферат: Порівняння функцій та їх застосування
Наслідок 1.
![]() (1.16)
(1.16)
і, зокрема, при ![]()
![]()
Дійсно, використовуючи неперервність логарифмічної функції, неперервність суперпозиції функцій і рівність (1.6), отримаємо:
![]()
Наслідок 2.
![]() (1.17)
(1.17)
Зокрема, якщо ![]() то
то
![]() (1.І8)
(1.І8)
Функція ![]() строго монотонна і неперервна на всій числовій осі, тому зворотна функція
строго монотонна і неперервна на всій числовій осі, тому зворотна функція ![]() також строго монотонна і неперервна при
також строго монотонна і неперервна при ![]() . Оскільки при
. Оскільки при ![]() маємо також і
маємо також і ![]() , то позначення
, то позначення ![]() і
і ![]() еквівалентні. Застосуємо для обчислення границі (1.17) правило заміни змінної.
еквівалентні. Застосуємо для обчислення границі (1.17) правило заміни змінної.
Поклавши ![]() , отримаємо
, отримаємо
![]()
ПОРІВНЯННЯ ФУНКЦІЙ
Всі, що розглядаються в цьому пункті, функції визначені в деякому фіксованому проколотому околі ![]() точки
точки ![]() розширеної числової прямої:
розширеної числової прямої: ![]() при чому цей окіл може бути і одностороній. Тому кожного разу не буде сказано, що
при чому цей окіл може бути і одностороній. Тому кожного разу не буде сказано, що ![]() .
.
Як ми вже знаємо, сума, різниця і добуток нескінченно малих функцій є також нескінченно малими функціями; цього не можна, взагалі кажучи, сказати про їх подільність: ділення однієї нескінченно малої на іншу може призвести до різноманітних випадків, як це показують нижче проведені приклади нескінченно малих при ![]() функцій
функцій ![]() і
і ![]() .
.
Нехай, наприклад ![]() і
і ![]() тоді
тоді
![]()
Якщо ж ![]()
![]() то
то ![]() а якщо
а якщо ![]()
![]() , то границя
, то границя ![]() не існує.
не існує.
Означення 1. Якщо для двох функцій f і g існують такі проколені околи ![]() і сталі
і сталі ![]() , що для всіх
, що для всіх ![]() виконується нерівність
виконується нерівність ![]() то функція f називається обмеженою порівнянно з функцією g на
то функція f називається обмеженою порівнянно з функцією g на ![]() і позначається:
і позначається:
![]()
(читається: ![]() є
є ![]() велике від
велике від ![]() при
при ![]() , прямучому до
, прямучому до ![]() ).
).
Наголосимо, що запис ![]() має тут інше, ніж звичайно, значення: він тільки вказує на те, що дана властивість має місце лише в деякому околі точки
має тут інше, ніж звичайно, значення: він тільки вказує на те, що дана властивість має місце лише в деякому околі точки ![]() ні про яку межу тут мови немає.
ні про яку межу тут мови немає.
Лема 3. Якщо ![]() і існує скінчена границя
і існує скінчена границя ![]() то
то ![]()
Доведення. З існування скінченої границі
![]() ,
,
слідує існування такого проколотого околу ![]() точки
точки ![]() що функція
що функція ![]() на ній обмежена, тобто є така стала
на ній обмежена, тобто є така стала ![]() , що для всіх
, що для всіх ![]() виконується нерівність
виконується нерівність ![]() а отже, і нерівність
а отже, і нерівність ![]() Це і означає, що
Це і означає, що ![]() ,
, ![]() .
.
Приклади. ![]() при
при ![]() , або
, або ![]() при
при ![]() ;
; ![]() при
при ![]() , або
, або ![]() при
при ![]() . Запис
. Запис ![]() при
при ![]() , означає, що функція
, означає, що функція ![]() обмежена в деякому околі точки
обмежена в деякому околі точки ![]() наприклад
наприклад ![]() при
при ![]() , або
, або ![]() , і, значить, функція
, і, значить, функція ![]() обмежена в околі точки
обмежена в околі точки ![]()
Означення 2. Якщо функції ![]() і
і ![]() такі, що
такі, що ![]() і
і ![]() при
при ![]() , то вони називаються функціями одного порядку при
, то вони називаються функціями одного порядку при ![]() , це записується у вигляді :
, це записується у вигляді :
![]()
Це поняття найбільш змістовне у тому випадку, коли функції f і g є або нескінченно малими, або нескінченно великими при ![]() . Наприклад, функції
. Наприклад, функції ![]() і
і ![]() є при
є при ![]() нескінченно малими одного порядку, бо
нескінченно малими одного порядку, бо
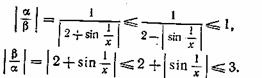
Лема 4. Якщо існує скінчена межа ![]() , то
, то ![]()
Доведення. Покладемо ![]() тоді
тоді ![]() і
і ![]() Отже з леми 3,
Отже з леми 3, ![]() при
при ![]() .
.
Оскільки ![]() існує такий проколений окіл
існує такий проколений окіл ![]() точки
точки ![]() ,що для всіх
,що для всіх ![]() маємо
маємо ![]() , а отже, і
, а отже, і ![]() Для
Для ![]() покладемо
покладемо ![]() тоді
тоді ![]() і
і ![]()
![]() . Тому, згідно леми 3
. Тому, згідно леми 3 ![]()