Реферат: Порівняння функцій та їх застосування

Наприклад візьмемо функцію і . Маємо (див. (1.1)), тому згідно доведеному, функції і одного порядку при .

Означення 3. Функціїи і називаються эквівалентними при , якщо в деякому проколеному околі точки визначена така функція , що

(1.20)

і

(1.21)

Відзначимо, що через властивість (1.21) знайдеться проколений окіл точки , у якій . Вважаючи бачимо, що умови (1.20) і (1.21) для вказаного проколеного околу рівносильні умовам

тобто як говорять, еквівалентність двох функцій має властивість симетричності.

Функції і , еквівалентні при , називаються також асимптотично рівними при Асимптотична рівність (еквівалентність) функцій позначається символом ~:

(1.22)

З сказаного вище слідує, що якщо при , то і при

Приклади. 1. при , Дійсно, припустивши , отримаємо:

і

2. ~ при . Дійсно, якщо 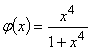, то

і

Якщо в деякому проколеному околі точки справедливі нерівності то умови (1.20) і (1.21) еквівалентні співвідношенню

а, отже, й умові

Щоб в цьому переконатися, достатньо покласти тоді, очевидно, для функції виконуються умови (1.20) і (1.21).

Якщо

f~g і g~f при (1.23)

то

f~h при (1.24)

Дійсно, з умов (1.23) виходить, що в деякому проколеному околі точки

де і, отже

,

де , тобто виконується асимптотична рівність (1.24).

З результатів пункту 1.1 слідує, що при справедлива наступна еквівалентність нескінченно малих:

З цієї еквівалентності випливають і більш загальні співвідношення, які сформулюємо у вигляді окремої леми.

Лема 4. Якщо функція така, що

(1.25)

то при ,

(1.26)

Доведення. Покажемо, наприклад, що

(1.27)

Нехай функція визначена в деякому проколеному околі точки Покладемо (вважаючи що належить цоьму околі)

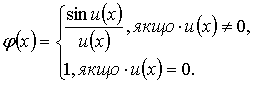(1.28)

Покажемо, що

(1.29)

Нехай задано Оскільки

(тут u — незалежна змінна), існує таке число що при виконується нерівність

Для вказаного в силу (1.25) знайдеться таке число , що для всіх , задовольняючих умову , виконується нерівністьо Отже, якщо і , то

Інакше кажучи, якщо і , то

(1.30)

Якщо ж і , то згідно (1.28) маємо і, отже, нерівність (1.30) очевидно також виконується.

Рівність (1.29) доведена, а оскільки з (1.28) випливає, що для всіх , то доведена справедливість асимптотичної рівності (1.27). Аналогічно доводиться і решта асимптотичні формули (1.26).

Означення 4. Якщо в деякому проколеному околі точки де , то функція називається нескінченно малою в порівнянні з функцією при , пишеться , (читається: є о мале від при , прямучому до ).