Реферат: Порівняння функцій та їх застосування

Через це означення запис означає просто, що функція є нескінченно малою при ,

Якщо при , та умову

можна переписати у вигляді

Таким чином, під при розуміється будь-яка функція така, що

У випадку, коли нескінченно мала при то говорять, що при є нескінченно мала більш високого порядку, ніж

Наприклад, при , або

Так само і при

Відзначимо, що якщо то і при Дійсно, нехай , де . Тоді функція обмежена в деякому проколеному околі точки точки і, значить, в вказаному проколеному околі, а це означає, що , .

Збираючи разом введені в цьому пункті основні поняття, отримаємо: нехай в деякому проколеному околі Ů=Ů(x) точки

тоді

якщо функція обмежена на , то

якщо '

якщо

При використовуванні рівності з символами О і о слідує мати на увазі, що вони не є рівністю в звичайному значенні цього слова. Так, якщо

то було б помилкою зробити звідси висновок, що як це було б у разі звичайної рівності. Наприклад, і при , але . Аналогічно, якщо

при

то було б помилкою зробити висновок, що

Річ у тому, що один і той же символ або може позначати різні конкретні функції. Ця обставина зв'язана з тим, що при визначенні символів і ми по суті ввели цілі класи функцій, що володіють певними властивостями (клас функцій, обмежених в деякому околі точки в порівнянні з функцією і клас функцій, нескінченно малих в порівнянні з f(x) при ) і було б правильнішим писати не і , а відповідно і о . Проте це призвело б до істотного ускладнення обчислень з формулами, в яких зустрічаються символи О і о. Тому ми збережемо колишній запис і , але завжди читатимемо цю рівність, відповідно до приведених вище визначень, тільки в одну сторону: зліва направо (якщо, звичайно, не обумовлено що-небудь інше). Наприклад, запис означає, що функція є нескінченно малою в порівнянні з функцією f при але зовсім не те, що всяка нескінченно мала по порівнянню з f функція рівна .

Як приклад на поводження з цими символами доведемо рівність

(1.31)

де с - стала.

Згідно сказаному, треба показати, що якщо , то . Дійсно, якщо , то , де0. Покладемо тоді де, очевидно і, значить, .

На закінчення відзначимо, що сказане про використовування символів О і о не виключає, звичайно, того, що окремі формули з цими символами можуть виявитися справедливими не тільки при читанні зліва направо, але і справа наліво; так, формула (1.31) при вірна і при читанні справа наліво.

Приклади.

1.;

тому

2.

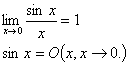
3., бо

4.Так як |1/x2| £ |1/x| при |x| ³ 1, то 1/x2 = O(1/x) при x ® ¥;

5.1/x = O(1/x2) при x® 0 так как |1/x|£ 1/x2 при |x|£ 1.

6.Функції f(x) = x(2+sin 1/x) g(x) = x x ® 0 являються нескінчено малими одного порядку при x® a , так як

f/g = (x(2+sin 1/x))/x = 2+sin 1/x = |2+sin 1/x| £ 3 Þ f=O(g), g/f = 1/|2+sin 1/x| £ 1 Þ g=O(f).

7. x2 = o(x) при x ® 0, так як limx ® 0x2/x = limx ® 0x = 0;

8.1/x2 = o(1/x) при x ® + ¥ так як limx ® ¥x/x2 = limx ® ¥1/x = 0

9.Знайти границю

Розв’язування. Використовуючи асимптотическое равенство (3) и асимптотическое равенство (1), а также учитывая, что x2 = o(x) при x® 0 (см. пример 15) и f=o(x2) является функцией o(x) при x® 0, найдем

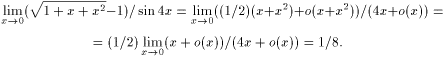
ЕКВІВАЛЕНТНІ ФУНКЦІЇ