Реферат: Скалярний добуток двох векторів, його властивості. Векторний добуток, його властивості. Змішаний добуток трьох векторів

Але .

Тепер вже легко записати, чому дорівнює .

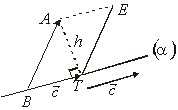
Рис.2.15

3. Векторно-скалярний (змішаний) добуток

трьох векторів

Коли мова йде про добуток трьох векторів і , можливі такі випадки:

Легко зрозуміти, що перший добуток є вектором, бо є скаляр, а добуток скаляра на вектор – вектор; у третьому випадку маємо векторний добуток , що множиться векторно на вектор , тобто зводиться до обчислення векторного добутку після того, як обчислено . У другому випадку справа зводиться до обчислення скалярного добутку після того, як обчислено .

З розглянутих трьох добутків змішаним є . Вивченням цього добутку і займемося.

Зрозуміло, що чисельно визначає площу паралелограма, побудованого на векторах і . Нехай . Тоді Чисельно . Але за означенням векторного добутку, а , бо вектор проектувався на вектор .

Отже чисельно можна вважати рівним об’єму паралелепіпеда, побудованого на векторах і із знаком “+” або “-” (рис .2.16). Об’єм, очевидно, буде додатним, якщо - гострий, а якщо цей кут тупий, то об’єм буде від’ємним.

Змішаний добуток, як правило, записують так: .

Змішаний добуток векторів, заданих координатами.

Нехай

Отже,

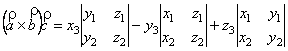
або

. (2.16)

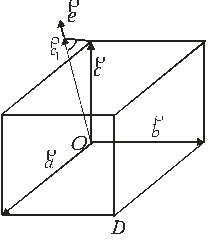
Рис. 2.16

Висновок. Векторно-скалярний добуток трьох векторів заданих своїми проекціями, дорівнює визначнику третього порядку, складеному з цих проекцій.

З формули (2.16), користуючись тим, що при перестановці двох сусідніх рядків визначника його знак змінюється на протилежний і відповідно переставляються множники у мішаному добутку, вірна така рівність:

тобто кругова перестановка трьох множників векторно-скалярного добутку не змінює його величини.

Перестановка двох сусідніх множників змінює знак добутку. Із формули (2.16) випливає також, що .

Якщо три вектори компланарні (паралельні одній і тій же площині), тоді і, значить, - необхідна і достатня умова компланарності векторів і . Цей факт очевидний і з геометричних міркувань. Об’єм паралелепіпеда в цьому випадку дорівнює нулю.

Приклад 1. Знайти найкоротшу віддаль між двома прямими, якщо одна з них проходить через точку паралельно вектору , а друга проходить через точку паралельно вектору (рис.2.17).

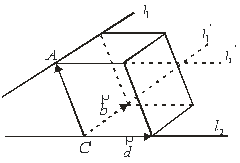
Рис. 2.17

Р о з в ’ я з о к. Побудуємо вектор і проведемо через точку пряму паралельну , а через точку пряму , паралельну прямій . Тоді прямі і та і визначають собою дві паралельні площини. Віддаль між цими площинами і буде найкоротшою віддаллю між прямими і . На векторах , і будуємо паралелепіпед. Його об’єм