Реферат: Основні правила диференціювання. Таблиця похідних

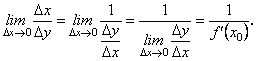
Отже, від функції в точці існує похідна:

(6.23)

Теорему доведено.

Якщо функція має похідну в довільній точці і

, то формула (6.23) справджується для цих точок

або, що те саме,

(6.24)

У формулі (6.24) похідні знаходяться за різними змінними: - похідна від до , а - похідна від до . Тому формулу (6.24) записують

(6.25)

Нижній індекс показує, за якою змінною знаходиться похідна.

Для зручності поміняємо у формулі (6.25) місцями і . Остаточно матимемо таку формулу для похідної від оберненої функції:

(6.26)

2. Похідні від елементарних функцій

Похідна від степеневої функції

Випадок натурального показника. Нехай , де - натуральне число. Тоді функція визначена на всій числовій осі. Отже, візьмемо довільну точку і надамо їй приросту . Тоді функція матиме приріст :

Розкриємо за формулою бінома Ньютона:

Знайдемо відношення

Перейшовши в цій рівності до границі при , дістаємо

Отже похідна від степеневої функції з натуральним показником існує і дорівнює

Випадок довільного показника. Нехай є довільне дійсне число. Тоді область існування функції залежить від .

Нехай - область існування функції . Візьмемо довільне , але (випадок розглянемо окремо). Тоді приріст дорівнює

Знайдемо відношення

або

(6.28)

де .

Перейдемо до границі у рівності (6.28) при . Зауважимо, що коли , то й . Тому

(6.29)

Обчислимо окремо

Для цього введемо таке позначення:

причому , якщо . Тоді звідки . Тоді

Проте внаслідок неперервності логарифмічної функції маємо

Отже,

Повертаючись до співвідношення (6.29), маємо

тобто якщо і , то

(6.30)

Розглянемо випадок, коли . Якщо , то точка не входить в область існування функції . Тому розглядатимемо і . Знайдемо приріст функції в точці :

тоді

Звідси випливає, що у випадку границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля, існує і дорівнює нулю:

Якщо , то границя не існує, тобто у випадку функція в точці похідної немає.

Проте, якщо формально у формулі (6.30) покласти , то дістанемо той самий результат.

Отже, для похідної від степеневої функції ми маємо таке правило: похідна від степеневої функції дорівнює показнику, помноженому на цю функцію з показником, на одиницю меншим.

3. Похідна від показникової та логарифмічної функцій

1. Нехай маємо показникову функцію .