Реферат: Основні правила диференціювання. Таблиця похідних

План

Основні правила диференціювання.

Похідні від елементарних функцій.

Похідна від степеневої функції.

Похідна від степеневої та логарифмічної функції.

Похідні від тригонометричних функцій.

Похідні від обернених тригонометричних функцій.

Похідна від складної функції.

1. Правила диференціювання

Операція знаходження похідної від даної функції називається диференціюванням цієї функції. Доведемо ряд теорем, які дають основні правила знаходження похідних від функцій.

10. Похідна від аргументу . Покладемо , тоді . Тому .

Отже, якщо , то

. (6.14)

1. Похідна від сталої функції .

Значення цієї функції у точках і рівні між собою при будь-якому . Тому приріст , а отже й .

Перейшовши до границі, в останній рівності при маємо

.

Границя відношення при існує і дорівнює нулю. Тому існує й похідна від цієї функції в довільній точці , яка теж дорівнює нулю, тобто

. (6.15) 3. Похідна від суми.

Теорема. Якщо функції в точці мають похідні, то функція також в цій точці має похідну і ця похідна дорівнює

. (6.16)

Д о в е д е н н я. Надамо деякого . Тоді функції матимуть прирости , функція - приріст . Знайдемо відношення

.

Перейдемо в цій рівності до границі при . Внаслідок того, що в точці згідно з умовою теореми мають похідну, то

, .

Тому

Отже, в цій точці існує похідна від функції і вона дорівнює .

Теорему доведено.

Наслідок. Похідна від суми скінченого числа функцій дорівнює сумі похідних від цих функцій, якщо похідні даних функцій існують, тобто

(6.17)

4. Похідна від добутку.

Теорема. Якщо функції в точці мають похідні, то в цій точці функція також має похідну:

. (6.18)

Д о в е д е н н я. Надамо деякого приросту . Тоді функції матимуть прирости , а функція приріст

Знайдемо відношення

Перейдемо в цій рівності до границі . За умови теореми

а

Отже,

Теорему доведено.

Наслідок. Постійний множник можна виносити за знак похідної, тобто, якщо , то

(6.19)

5. Похідна від частки.

Теорема. Якщо функції в точці мають похідні і , то функція також у точці має похідну і похідна дорівнює

(6.20)

Д о в е д е н н я. Надамо приросту . Тоді функції матимуть відповідно прирости , а функція - приріст

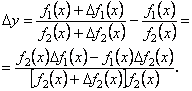
Знайдемо відношення

За умовою теореми

а , тому

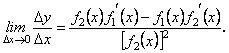
Теорему доведено.

Наслідок 1. Якщо знаменник дробу - стала величина, то

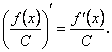(6.21)

Наслідок 2. Якщо чисельник дробу стала величина, то

(6.22)

6. Похідна від оберненої функції.

Теорема. Нехай функція задовольняє всім умовам теореми про існування оберненої функції і в точці має похідну . Тоді обернена до неї функція у точці має також похідну: .

Д о в е д е н н я. Надамо приросту . Тоді функція дістане приріст , причому, внаслідок монотонності функції , матимемо , якщо . Тоді відношення можна записати так: Перейдемо в цій рівності до границі при . Внаслідок неперервності оберненої функції , тобто