Реферат: Інтегровані типи д-р 1-го порядку, розвязаних відносно похідної

Розглянемо два методи интигрування неоднорідного ДР (2.67).

Метод Лагранжа (варіації довільної сталої).

Розвязок шукаємо у вигдяді (2.70). Підставимо (2.70) в (2.62). . Звідки ,

. Остаточно маємо (2.71).

загальний розв’язок ДР (2.62), який записаний через дві квадратури. Довільна стала входить завжди в загальний розв’язок лінійно.

Метод Ейлера заключається в тому, що ліва частина ДР (2.62) представляється у вигляді точної похідної шляхом домноження на деяку функцію Визначимо звідки тобто (ф-я) називається інтерувальним множником). Тому (2.72) звідки. З останнього співвідношення отримуємо ф-лу (2.71).

Загальний розв’язок при умові можна записати в Формі Коші .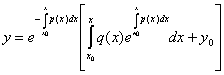

Пр.2.9 Знайти загальний розв’язок ДР

Це лінійне однорідне ДР .

Пр.2.10 Розв’язати ДР .

За формулою (2.71)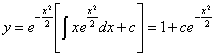

д) Рівняння Бернуллі Це рівняння має вигляд (2.74)

Рівняння (2.74) завжди інтегрується в квадратурах шляхом підстановки (2.75). Так як , то домножимо (2.74) на , маємо (2.76) яке вже являється лінійним.

При рівняння Бернуллі має особливий розв’язок. При розв’язок міститься в загальному розв’язку при. При не являється розв’язком ДР (2.74)

Пр.2.11 Розв’язати ДР , , ,. Отже - загальний розвязок нашого р-ня.

Відомо, що деференц. – ліннійне р-ня.

Р-ня зводиться до лінійного заміною.