Реферат: Інтегровані типи д-р 1-го порядку, розвязаних відносно похідної

а). Неповні р-ня. ДР, яке не містить шуканої функції.

Має вигляд

, (2.33)

Припустимо, що f(x) являється неперервною на функцією.

Тоді ф-я

(2.34)

являэться загальним розв`язком д-р (1) в області a < x < b, -< y < + .(2.35)

Особливих розвязків ДР (2.33) немає.

Разом з ДР (2.33) розглянемо початкові умови (2.36)

Проінтегруємо ДР (2.34) від до x

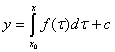
Знаходимо с з умови (2.36)

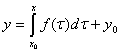(2.37) - загальний розвязок ДР (2.33) в формі Коші.

Якщо f(x) - неперервна на за виключенням точки , в якій приймає нескінченне значення, то замість ДР (2.34) будемо розглядати р-ня

(2.331)

Пряма являється розвязком ДР (2.331) і ми цей розвязок повинні приєднати до розвязку ДР (2.33). Цей розвязок може бути частинним або особливим в залежності від того зберігається чи порушується в будь-якій його точці єдність. Якщо - частинний розвязок, то його часто можна отримати з загального при нескінченних заначеннях с, якщо ж він являється особливим, то його отримують з загального при .

Р-ня, яке не містить незалежної змінної має вигляд

(2.38)

Припускаємо, що ф-я визначена і неперевна на інтервалі . Замість (2.38) розглянемо ДР

(2.39)

ДР (2.39) не містить шуканої функції і воно розвязується аналогічно ДР (2.33).

Якщо , y є (c,d), то

(2.40) – загальний рохвязок ДР (2.39) в області

c < y < d, -< x < + .

Аналогічно 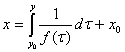(2.41) - загальний інтеграл в формі Коші.

Якщо неперервна на (c,d) і приймає нульове значення при , то ми повинні розглядаті ДР (2.38). Розвязок буде частинним, якщо в кожній його точці зберігається єдиність, і осоюливим, якщо в кожній його точці порушується єдиність. Якщо частинний розвязок, то ми його отримуємо при нескінченних значеннях , якщо особливий, то при .

Якщо в тоцчі перетворюється в нескінченність , то розглянемо ДР (2.39), яке має неперервну праву частину на (c,d). При цьому ДР на має єдиний розвязок .

Пр. 2.5

Розглянемо ДР .

Область визначення : .

Поскільки в т. дотичні паралельні осі OY, то розвязок в єдиний , .

б) Рівняння з відокремлюванними змінними.

Розглянемо р-ня в диференціалах виду

(2.42),

де - неперервні ф-ї своїх аргументів.

Деференціальне р-ня (2.42) називається р-ням з відокремленими змінними. Його можна переписати данним чином . Звідки маємо загальний розвязок в квадратурах. (2.43).

Якщо треба записати розвязок задачі Коші, то записують так 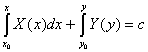. З умови (2.36) визначають . Отже 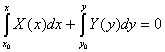(2.44) – розвязок задачі Коші (2.36), (2.42). При данних припущеннях особливих розвязків ДР (4.42) не має.

Рівняння вигляду

(2.45) –

називають р-ням з відокремлюваними змінними.

Припустимо, що , тоді розділемо обидві частини рівняння (2.45) на , отримуємо

(2.46).

Аналогічно записуємо

(2.47) –

загальний розвязок ДР (2.45) і

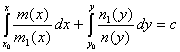(2.48) –

розвязок задачі Коші (2.36) , (2.45). При діленні на ми можемо загубити розвязки, які визначаються рівняннями ,. Дійсно, нехай , то

отже - розвязок ДР (2.45).

Аналогічно .

Якщо ці розвязки не входять в (2,47) при деяких , то вони представляють собою особливі розвязки ДР (2.45).

З розвязку ми повинні викинути точку , так як в точці ДР (2.45) не визначає нахил поля . По тій же причині з розвязку викидають точку .

Таким чином розвязки і примикають до точки і можуть бути особливими. Других особливих розвязків не має.

Пр. 2.6.

Знайти загальний розвязок ДР:

.

Розвязок:

. .

.

.

.

.

в). Однорідні і узагальнено-однорідні ДР.

Розглянемо р-ня в диференціалах

(2.5),

в якому ф-ії і являються однорідними функціями одніеї і тієї ж степені однорідності.