Реферат: Інтегровані типи д-р 1-го порядку, розвязаних відносно похідної

Означення 2.4: ф-я називаеться однорідною степеню ,

якщо (2.49).

Якщо (2.49) виконуються при , то ф-я називаеться додатню-однорідною.

Однорідне р-ня завжди можна звести до рівняння вигляду

(2.50),

в якому функція однорідна функція нулбового виміру.

Однорідні рівняння завжди інтегруються в квадратурах заміною (2.51). При цьому р-ня (2.5) приводиться до рівняння з відокремлюваними змінними. Дійсно

,

,

,

,

,

,

(2.52), де .

При діленні ми могли загубити розвязок , де - корені рівняння (2.53).

Отже півпрямі примикають до початку координат. Ці розвязки можуть міститися в формулі загального розвязку, але можуть бути і особливими. Особливими можуть бути також півосі осі . Других особливих розвязків ДР (2.5) не має.

Рівняння вигляду(2.54) зводиться до однорідного. Якщо , то це однорідне рівняння.

Припустимо, що хоч одне з чисел не дорівнюють 0. Можливі два випадки:

Перший) Проводимо заміну (2.55), де - нові змінні, - параметри. Тоді (2.56).

Параметри вибираємо згідно системи (2.57). Так як то система (2.57) має єдиний розвязок. Таким чином, ми прийшли до однорідного ДР (2.58).

Другий) . В цьому випадку , тобто . Тому (2.59)

Заміною ДР (2.59) приводимо до рівняння з відокремленими змінними (2.60).

Пр 2.7 Знайти загальний розвязок ДР

Це однорідне рівняння, . Зробимо заміну ,

, .

Отже - загальний розвзок нашого рівняння.

ДР (2.5) називається узагальнено-однорідним, якщо існує таке число , при якому ліва частина цього ДР (2.5) стає однорідною функцією від велечин в припущенні, що __ мають віжповідно виміри: перший, -ий, нульвий , -ий. При має просто однорідне рівняння.

В цьому випадку ДР (2.5) заміною (2.61) зводитьчя до р-ня з відоктремлюванними змінними. При р-ня (2.5) являється р-ням з розділеними зміними. Особліви розвязки досліджуються аналогічно.

Пр 2.8 Розвязати ДР:

Знайдемо чило для данного випадку . Отже , ,формула

Звідки загальний розвязок.

г) Лінійні р-ня порядку.

ДР вигляду (2.62) називаються лінійними ДР порядку.

При воно називається однорідним

Формула (2.63). Так як ліва частина ліній на і однорідна відносно і . Р-ня (2.62) при називається неоднорідним. ДР (2.63) інтирується в квадратурах, так як воно являється ДР з відокремлюваними змінними.. Звідки (2.64).

Якщо то (2.65)

Загальні властивості ОДР :

Якщо та неперервні, то згідно теореми Пікара розвязок задачі Коші для ДР (2.63) існує і являється єдиним;

ЛДР (2.63) не має особливих розвязків;

ІК ОДР (2.63) не можуть пееретинати вісь , так як в противному випадку нарушалися б умови єдиності розвязку задачі Коші;

ДР (2.63) інваріантно відносно перетворення ;

Дійсно: формула , .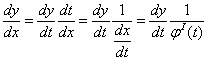

ДР (2.63) іваріантно відносно заміни (2.66) де -новазмінна, та - неперервні ф-ї, на . Тоді . Якщо - частинний розвязок ДР (2.63), то (2.67), де - константа, являється загальним його розвязком. Справедлива теорема.

Теорема (2.3) (про структуру розвязку лінійного неоднорідного ДР): Якщо - частинний розвязок неоднорідного ДР (2.62), а ДР (2.64)- загальний розвязок ОДР (2.63) то сума (2.68) являється загальним розвязком неоднорідного ДР (2.62).

Теорема доводиться безпосередньою подстановкою (2.68) в

р-ня (2.62).

Якщо відомо два частинних розвязки ДР (2.62), то загальний його розвязок записується без квадратур (2.69).