Реферат: Диференціальні рівняння першого порядку (з відокремлюваними змінними, однорідні, лінійні, Бернуллі)

де - абсциса будь-якої точки в області існування розв’язку, а - поки що невідома функція, яка залежить лише від . Знайдемо похідну , користуючись формулою (12.28):

(12.29)

Враховуючи, що і користуючись умовою (12.26) для заміни підінтегральної функції, з (12.29) отримуємо

Отже, або

Звідси , або ,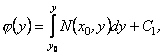

де - довільна стала. Підставляючи знайдену функцію у вираз (12.28), отримаємо

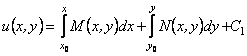Це дозволяє записати загальний розв’язок рівняння (12.25) (або те ж саме рівняння (12.27)) у вигляді:

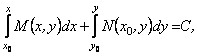
- довільна стала.

Зауваження. На практиці зручніше продиференціювати

рівність (12.28) за , потім замінити відомою функцією , а далі – визначити та .

Приклад . Розв’язати рівняння

Р о з в ’ я з о к. Позначимо

і переконаємося, що це – рівняння в повних диференціалах. Справді, частинні похідні і рівні між собою:

Отже, умова (12.26) виконується. Для знаходження функції про інтегруємо рівність .

Маємо .

Звідси визначимо похідну: та прирівняємо її до відомої функції :

Отже, і, ,

де - довільна стала.

Функцію знайдено:

Загальний інтеграл рівняння має вигляд .

Розглянемо питання про можливість зведення рівняння виду (12.25), для якого не виконується умова (12.26), до рівняння в повних диференціалах. Домножимо обидві частини рівняння (12.25) на деяку функцію таку, що рівняння

(12.30)

буде рівнянням у повних диференціалах. Згідно з доведеним для цього необхідно і достатньо, щоб виконувалась рівність, аналогічна рівності (12.26):

або

Зведемо подібні члени

Поділивши обидві частини цього рівняння на та врахувавши, що , отримаємо

(12.31)

Це рівняння в частинних похідних відносно . Розв’язати його – це завдання не простіше, ніж інтегрування вихідного рівняння. Розглянемо два частинні випадки, коли рівняння (12.31) спрощується і його можна розв’язати.

1) Нехай шуканий інтегральний множник залежить лише від : .

Тоді , і рівняння (12.31) набуває вигляду

(12.32)

Якщо права частина цього рівняння не залежить від , то воно легко інтегрується.

2) Якщо інтегральний множник є функцією тільки від : , то , а .

Тоді рівняння (12.31) можна подати таким чином:

(12.33)

Якщо вираз справа залежить лише від , рівняння (12.33) інтегрується.

Приклад 2. Розв’язати рівняння . Зауважимо, що в розглянутому випадку .

Р о з в ’ я з о к. Знайшовши частинні похідні

переконуємося, що умова (12.26) не виконується.

Спробуємо підібрати інтегральний множник виду . Рівняння (12.32) набуває вигляду

Вираз у правій частині останньої рівності залежить і від , і від . Отже, інтегрального множника вигляду не існує.

Припустимо, що , і складемо рівняння (12.33):

Оскільки вираз у правій частині цієї рівності залежить від , рівняння інтегрується. Знайдемо один з його частинних розв’язків:

, звідки . Перевіримо, чи множник знайдено правильно. Для цього домножимо обидві частини вихідного рівняння на та переконаємося, що коефіцієнти отриманого рівняння задовольнятимуть умові (12.26). Маємо