Реферат: Диференціальні рівняння першого порядку (з відокремлюваними змінними, однорідні, лінійні, Бернуллі)
![]() .
.
Тоді загальний розв’язок рівняння набуває вигляду
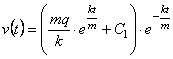 ,або
,або ![]() .
.
Поклавши тут ![]() і
і ![]() , знайдемо, що
, знайдемо, що ![]() .
.
Отже, частинний розв’язок поставленої задачі матиме вигляд
 .
.
Приклад 3. З фізики відома залежність між силою стуму ![]() та електрорушійною силою
та електрорушійною силою ![]() в колі, яке має опір
в колі, яке має опір ![]() та самоіндукцію
та самоіндукцію ![]() (
(![]() та
та ![]() - сталі):
- сталі):
![]() .
.
Якщо ![]() , то це рівняння повністю збігається з диференціальним рівнянням, розглянутим у прикладі 2, хоч описувані процеси зовсім різні.
, то це рівняння повністю збігається з диференціальним рівнянням, розглянутим у прикладі 2, хоч описувані процеси зовсім різні.
Нехай ![]() . Тоді відносно
. Тоді відносно ![]() маємо диференціальне рівняння, яке зручно записати у вигляді
маємо диференціальне рівняння, яке зручно записати у вигляді
![]() .
.
Знайдемо загальний розв’язок цього лінійного рівняння. Нехай ![]() , де
, де ![]() та
та ![]() - невідомі функції. Тоді
- невідомі функції. Тоді ![]() Після підстановки в рівняння
Після підстановки в рівняння ![]() та
та ![]() маємо:
маємо: ![]()
або ![]() .
.
Невідому функцію ![]() знайдемо з рівняння
знайдемо з рівняння
![]() ,звідки
,звідки ![]() . Величина
. Величина ![]() визначається з рівності
визначається з рівності ![]() ,
,
звідки
![]() ,
,
де ![]() довільна стала. Позначимо інтеграл, що фігурує справа, через
довільна стала. Позначимо інтеграл, що фігурує справа, через ![]() :
: ![]() . Інтегруючи двічі частинами, отримаємо
. Інтегруючи двічі частинами, отримаємо
![]() ,
,
а функцію ![]() визначимо за допомогою рівності
визначимо за допомогою рівності
![]() .
.
Отже, сила струму ![]() визначається виразом
визначається виразом
![]() .
.
12.5. Рівняння Бернуллі
Диференціальне рівняння виду
![]() , (12.24)
, (12.24)
в якому ![]() неперервні функції, а число
неперервні функції, а число ![]() відмінне від
відмінне від
нуля та одиниці, називається рівнянням Бернуллі (при ![]()
маємо лінійне рівняння, а при ![]() - рівняння з відокремлюваними
- рівняння з відокремлюваними
змінними).
Покажемо, що рівняння Бернуллі зводиться до лінійного диференціального рівняння першого порядку. Для цього поділимо ліву й праву частини рівняння (12.24) на ![]() :
:
![]()
та виконаємо заміну змінної ![]() . Оскільки
. Оскільки
![]() ,
,
диференціальне рівняння Бернуллі перетворюється на рівняння
![]()
яке є лінійним. Проінтегрувавши його одним з описаних раніше способів і повернувшись від ![]() до попередньої змінної
до попередньої змінної ![]() , можна отримати розв’язок рівняння Бернуллі.
, можна отримати розв’язок рівняння Бернуллі.
Зауважимо, що зручніше розв’язувати рівняння Бернуллі, не зводячи його до лінійного, за допомогою підстановки ![]() , тобто так само, як і лінійне неоднорідне рівняння.
, тобто так само, як і лінійне неоднорідне рівняння.
Покажемо це на прикладі.
Приклад . Розв’язати рівняння Бернуллі
![]() .
.
Р о з в ’ я з о к. Будемо шукати невідому функцію ![]() у вигляді.
у вигляді.![]() . Підстановка цієї функції у рівняння приводить до рівності
. Підстановка цієї функції у рівняння приводить до рівності ![]() або
або
![]() .
.
Функцію ![]() знайдемо із співвідношення
знайдемо із співвідношення ![]() , яке отримується, якщо вираз у дужках прирівняти до нуля:
, яке отримується, якщо вираз у дужках прирівняти до нуля: ![]() . Відносно
. Відносно ![]() отримується рівняння з відокремлюваними змінними
отримується рівняння з відокремлюваними змінними
![]() , загальний інтеграл якого буде таким:
, загальний інтеграл якого буде таким:
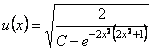 ,
,
де ![]() довільна стала. Отже, відповідь
довільна стала. Отже, відповідь
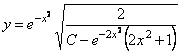 .
.
12.6. Рівняння в повних диференціалах.
Інтегруючий множник
Означення. Диференціальне рівняння вигляду
![]() (12.25)
(12.25)
називається рівнянням у повних диференціалах, якщо ![]()
![]() - неперервні диференційовані функції, для яких
- неперервні диференційовані функції, для яких
виконується співвідношення
![]() , (12.26)
, (12.26)
причому ![]() та
та ![]() - також неперервні функції.
- також неперервні функції.
Покажемо, що коли ліва частина рівняння (12.25) є повним диференціалом деякої функції ![]() , то виконується умова (12.26), і навпаки, з виконання умови (12.25) випливає, що ліва частина рівняння (12.25) – повний диференціал (вперше цю умову отримав член Петербурзької академії наук Л.Ейлер (1707-1783)).
, то виконується умова (12.26), і навпаки, з виконання умови (12.25) випливає, що ліва частина рівняння (12.25) – повний диференціал (вперше цю умову отримав член Петербурзької академії наук Л.Ейлер (1707-1783)).
Справді, нехай зліва у рівнянні (12.25) стоїть повний диференціал, тобто ![]() .
.
Оскільки
![]() ,
,
маємо
![]()
Тоді частинні похідні ![]() та
та ![]() визначаються за формулами
визначаються за формулами
 .
.
Оскільки зліва в цих рівностях згідно з умовою записані неперервні функції, то це означає, що й праві частини, тобто ![]() та
та
![]() , також неперервні. Звідси випливає, що
, також неперервні. Звідси випливає, що ![]() , що й доводить рівність (12.26).
, що й доводить рівність (12.26).
Припустимо тепер, що умова (12.26) виконується, і знайдемо функцію ![]() , завдяки якій диференціальне рівняння (12.25) можна подати у формі
, завдяки якій диференціальне рівняння (12.25) можна подати у формі
![]() (12.27)
(12.27)
Оскільки ![]() , то інтегруючи, маємо
, то інтегруючи, маємо
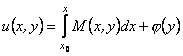 (12.28)
(12.28)