Реферат: Числові послідовності
![]()
![]()
Теорема 4. Нехай члени послідовностей ![]() ,
, ![]() ,
, ![]() при всіх значеннях
при всіх значеннях ![]() задовольняють нерівності
задовольняють нерівності ![]() і
і ![]() Тоді
Тоді ![]()
4. Нескінченно малі та нескінченно великі числові послідовності
Введемо поняття нескінченно малих та нескінченно великих послідовностей і встановимо зв’язок між ними.
Означення. Числова послідовність ![]() називається нескінченно малою, якщо
називається нескінченно малою, якщо
![]()
![]() (5.5)
(5.5)
що те саме при ![]()
Означення. Числова послідовність ![]() називається нескінченно великою, якщо
називається нескінченно великою, якщо
![]()
![]() (5.6)
(5.6)
Цей вираз записують так:
![]()
Теорема 1. Якщо послідовність ![]() нескінченно мала і
нескінченно мала і ![]() при всіх
при всіх ![]() то послідовність
то послідовність ![]() - нескінченно велика. Якщо послідовність
- нескінченно велика. Якщо послідовність ![]() нескінченно велика і
нескінченно велика і ![]() при всіх
при всіх ![]() то послідовність
то послідовність ![]() - нескінченно мала.
- нескінченно мала.
Теорема 1. Для того щоб послідовність ![]() мала границю, яка б дорівнювала
мала границю, яка б дорівнювала ![]() необхідно і достатньо, щоб існувала така нескінченно мала послідовність
необхідно і достатньо, щоб існувала така нескінченно мала послідовність ![]() що
що
![]() (5.7)
(5.7)
Зауваження. Розглянемо арифметичні операції над числовими послідовностями: додавання, віднімання, множення та ділення.
Нехай маємо дві послідовності :![]()
![]()
![]()
![]()
![]()
![]() (5.8)
(5.8)
та
![]()
![]()
![]() (5.9)
(5.9)
Тоді додавання, віднімання та множення послідовностей (5.8), (5.9) виконуються додаванням, відніманням чи множенням відповідних членів цих послідовностей.
Якщо всі ![]()
![]() то частка від ділення послідовності (5.8) на послідовність (5.9) визначається як послідовність
то частка від ділення послідовності (5.8) на послідовність (5.9) визначається як послідовність![]()
![]()
![]() члени якої
члени якої ![]()
![]()
Символічно ці дії познаються так:
![]()
![]()
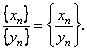
Теорема 2. Алгебраїчна сума двох нескінченно малих є нескінченно мала.
Наслідок 1. Алгебраїчна сума скінченої множини нескінченно малих є нескінченно мала.
Теорема 2. Добуток нескінченно малої числової послідовності на послідовність обмежену є нескінченно мала числова послідовність.
Наслідок 2. Добуток сталої величини на нескінченно малу числову послідовність є нескінченно мала числова послідовність.
Наслідок 3. Добуток скінченого числа нескінченно малих числових послідовностей є нескінченно мала числова послідовність.
5. Основні теореми про границі
Наведемо теореми, якими користуються для знаходження границі числових послідовностей.
Теорема 1. Алгебраїчна сума двох збіжних послідовностей ![]() і
і ![]() є збіжна послідовність, її границя дорівнює відповідній сумі границь даних послідовностей.
є збіжна послідовність, її границя дорівнює відповідній сумі границь даних послідовностей.
Д о в е д е н н я. Нехай ![]()
![]() Тоді
Тоді
![]()
![]()
де ![]() і
і ![]() - нескінченно малі послідовності.
- нескінченно малі послідовності.
Додавши почленно ці рівності, дістанемо:
![]()
Отже, вираз ![]() ми подали у вигляді суми сталого числа
ми подали у вигляді суми сталого числа ![]()
і нескінченно малої ![]() Тому існує
Тому існує ![]() та
та
![]()
Зауваження . Теорема справедлива й для випадку всякого скінченого числа збіжних числових послідовностей.
Теорема 2. Добуток двох збіжних послідовностей ![]() і
і ![]() є збіжна послідовність, її границя дорівнює добутку границь даних послідовностей.
є збіжна послідовність, її границя дорівнює добутку границь даних послідовностей.
Д о в е д е н н я. За умовою теореми ![]()
![]()
Тому ![]()
![]() де
де ![]()
![]() - нескінченно малі послідовності.
- нескінченно малі послідовності.
Тоді ![]()
Із властивостей нескінченно малих виводимо, що послідовність
![]() - нескінченно мала.
- нескінченно мала.
Звідси
![]() тобто
тобто ![]()
Теорему доведено.
Зауваження. Теорема справедлива й у випадку добутку всякого скінченого числа збіжних послідовностей.
Наслідок 1. Якщо послідовність ![]() має скінчену границю, то при всякому сталому
має скінчену границю, то при всякому сталому ![]() маємо:
маємо:
![]()
або сталий множник можна виносити за знак границі.
Наслідок 2. Якщо ![]() і
і ![]() - натуральне число,
- натуральне число,
то
![]()
Теорема 3. Якщо послідовності ![]() і
і ![]() збігаються,
збігаються, ![]()
![]() причому
причому ![]()
![]() і
і ![]() то
то
послідовність ![]() збігаються і її границя дорівнює відношенню
збігаються і її границя дорівнює відношенню
границь послідовностей ![]() та
та ![]()
Д о в е д е н н я. За умовою теореми
![]()
![]()
де ![]()
![]() - нескінченно малі послідовності.
- нескінченно малі послідовності.
Оскільки ![]() то
то ![]()
![]() де
де ![]() - стале число.
- стале число.
Надалі обмежимося тими членами послідовності ![]() які задовольняють попередній нерівності. Тоді
які задовольняють попередній нерівності. Тоді
![]() .
.
Послідовність![]() є обмежена, оскільки
є обмежена, оскільки ![]()
Послідовність ![]() є нескінченно мала. Таким чином,
є нескінченно мала. Таким чином, 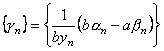 є нескінченно мала.
є нескінченно мала.
Тому ![]()
Теорему доведено.
При вивчені основних теорем про границі ми вважали, що числові послідовності ![]() і
і ![]() мають скінченні границі, причому при доведенні теореми про границю частки вважали, що границя дільника не дорівнює нулю.
мають скінченні границі, причому при доведенні теореми про границю частки вважали, що границя дільника не дорівнює нулю.
Розглянемо випадок, коли ![]() і
і ![]() є нескінченно великі числові послідовності, тобто
є нескінченно великі числові послідовності, тобто
![]()
![]()
Легко бачити, що арифметична сума і добуток цих послідовностей є також нескінченно велика числова послідовність. Проте нічого конкретного в загальному випадку не можна сказати про частку від ділення та різницю цих послідовностей. Частка від ділення таких послідовностей залежно від закону зміни ![]() і
і ![]() може
може
поводити себе по-різному. Кожного разу відношення ![]() треба досліджувати. Тому говорять, що відношення
треба досліджувати. Тому говорять, що відношення ![]() якщо
якщо ![]()
![]() є невизначеність. І цю невизначеність символічно позначають так:
є невизначеність. І цю невизначеність символічно позначають так: ![]()
Приклади.
1. Знайти ![]()
Р о з в ’ я з о к. Розкрити невизначеність ![]() В цьому випадку поступають так: чисельник і знаменник ділять на
В цьому випадку поступають так: чисельник і знаменник ділять на ![]() (від цього дріб не змінюється ), а потім застосовують теореми про границі частки і суми. Наведемо повний запис обчислення границі:
(від цього дріб не змінюється ), а потім застосовують теореми про границі частки і суми. Наведемо повний запис обчислення границі: 

2. Знайти ![]()
Р о з в ’ я з о к. ![]()

3. Знайти ![]()
![]()
Р о з в ’ я з о к.

Сказане про частку стосується й різниці двох нескінченно великих числових послідовностей. Якщо ![]()
![]() то різницю
то різницю ![]() називають невизначеністю виду
називають невизначеністю виду ![]()
Приклад. Знайти ![]()
Р о з в ’ я з о к. Тут маємо невизначеність виду ![]() Для її розкриття позбавляємося ірраціональності у чисельнику.
Для її розкриття позбавляємося ірраціональності у чисельнику.
Матимемо ![]()
З аналогічним фактом ми зустрічаємось у випадку відношення двох нескінченно малих числових послідовностей. Якщо ![]()
![]() то частка від ділення
то частка від ділення ![]() може також поводити себе по – різному. Цю невизначеність називають невизначеністю виду
може також поводити себе по – різному. Цю невизначеність називають невизначеністю виду ![]() Цю, а також й інші невизначеності розглянемо в наступних параграфах.
Цю, а також й інші невизначеності розглянемо в наступних параграфах.
6. Границя монотонної числової послідовності
Основні теореми про границі дають змогу встановлювати та знаходити числове значення границі заданої числової послідовності за допомогою границь інших числових послідовностей, певним чином пов’язаних з розглядуваною. Проте в деяких випадках як теоретичного, так і практичного характеру не завжди можна використати ці теореми. Тому доводиться застосовувати інші способи, зокрема ознаки збіжності числових послідовностей.
Теорема 1. Якщо послідовність
![]()
![]()
![]() (5.10)
(5.10)
є монотонно зростаюча (спадна) і обмежена зверху (знизу), то вона збіжна.
5. Порівняння нескінченно малих величин
Іноді доводиться розглядати не одну, а декілька нескінченно малих функцій в даній точці. Такі функції порівнюють між собою за допомогою границі їх відношення. Знайти границю такого відношення за відомими теоремами про нескінченно малі і про границі не можна. Це не випадково. Відношення двох нескінченно малих, залежно від характеру зміни порівнюваних між собою нескінченно малих, може вести себе по-різному: воно може бути або величиною, що прямує до скінченої, відмінної від нуля границі, або величиною нескінченно малою, або нескінченно великою, або величиною, яка має границі.
Кожне із цих чотирьох випадків має свою назву. Нехай ![]() і
і ![]() є нескінченно малі функції в точці
є нескінченно малі функції в точці ![]() .
.
Означення.1. Якщо
![]() ,
,
то ![]() і
і ![]() в точці
в точці ![]() називаються нескінченно малими однакового порядку малості.
називаються нескінченно малими однакового порядку малості.
Приклади.
1. Нехай ![]() . При
. При ![]() і
і
і ![]() прямують до нуля. Знайдемо
прямують до нуля. Знайдемо
![]()
Отже, функції ![]() і
і ![]() є нескінченно малі однакового порядку малості в точці
є нескінченно малі однакового порядку малості в точці ![]() .
.
2. Нехай
![]()
![]() і
і ![]() .
.
Знайдемо
![]() .
.
Отже, функції ![]() і
і ![]() на нескінченності однакового порядку малості.
на нескінченності однакового порядку малості.
3. Нехай ![]() ,
,
![]() і
і ![]() .
.
Знайдемо
![]() .
.
Отже, функції ![]() і
і ![]() при
при ![]() нескінченно малі однакового порядку малості.
нескінченно малі однакового порядку малості.
Означення 2. Якщо
![]() ,
,
то ![]() називається нескінченно малою вищого порядку малості, ніж
називається нескінченно малою вищого порядку малості, ніж ![]() . При цьому
. При цьому ![]() - нескінченно мала нижчого порядку малості, ніж
- нескінченно мала нижчого порядку малості, ніж ![]() .
.
Приклади.
1. Нехай ![]()
![]() . Тоді
. Тоді ![]() і
і ![]() в
в
точці ![]() є нескінченно малі функції. Знайдемо
є нескінченно малі функції. Знайдемо
![]()
Отже, в цьому випадку ![]() є нескінченно мала вищого порядку, ніж
є нескінченно мала вищого порядку, ніж ![]() .
.
2. ![]() ,
, ![]() ,
, ![]() і
і ![]() - нескінченно малі при
- нескінченно малі при![]() . Знайдемо
. Знайдемо
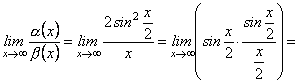

Отже, при ![]()
![]() є нескінченно мала вищого порядку, ніж
є нескінченно мала вищого порядку, ніж ![]() .
.
Означення 3. Якщо
![]() ,
,
то ![]() називається нескінченно малою більш нижчого порядку малості, ніж
називається нескінченно малою більш нижчого порядку малості, ніж ![]() .
.
Приклад.
Нехай ![]() ,
, ![]() . При
. При ![]()
![]() і
і ![]() - нескінченно малі. Знайдемо
- нескінченно малі. Знайдемо

Отже, при ![]()
![]() є нескінченно малою нижчого
є нескінченно малою нижчого
порядку малості, ніж ![]() .
.
Означення 4. Якщо границі відношення ![]() і
і ![]() не існує (ні скінчена, ні нескінченна), то
не існує (ні скінчена, ні нескінченна), то ![]() і
і ![]() називаються не порівнювальними нескінченно малими.
називаються не порівнювальними нескінченно малими.
Означення 5. Якщо
![]() ,
,
то ![]() і
і ![]() в точці
в точці ![]() називаються еквівалентними, і записуються :
називаються еквівалентними, і записуються : ![]() ~
~ ![]() .
.
Приклади.
1. Нехай ![]() ,
, ![]() . Тоді
. Тоді ![]() і
і ![]() в точці є нескінченно малі. Оскільки
в точці є нескінченно малі. Оскільки ![]() (доведення буде дано в наступній темі), то
(доведення буде дано в наступній темі), то ![]() і
і ![]() є еквівалентні величини, тобто
є еквівалентні величини, тобто ![]() ~
~ ![]() .
.
2. Довести, що в точці ![]() :
:
| а) |
| б) |
|
| в) |
| г) |
|
| д) |
| е) |
|
| ж) |
| з) |
|