Реферат: Розвиток творчих здібностей учнів на уроках математики

Отже, весь процес розв'язування за­дачі можна розділити на вісім етапів:

1-й етап - аналіз задачі;

2-й етап - схематичний запис задачі;

3-й етап - пошук способу розв'язу­вання задачі;

4-й етап - виконання розв'язування задачі;

5-й етап-перевірка розв'язку задачі;

6-й етап - дослідження задачі;

7-й етап - формулювання відповіді задачі;

8-й етап - аналіз розв'язування за­дачі.

Математичні задачі, для розв'язуван­ня яких в шкільному курсі математи­ки існують готові правила, або ці пра­вила безпосередньо випливають з оз­начень чи теорем, що визначають програму розв'язування цих задач у вигляді послідовності кроків, нази­вають стандартними. При цьому пе­редбачається, що для виконання ок­ремих кроків розв'язування стандарт­них задач в курсі математики існують конкретні правила.

Процес розв'язування стандартних задач має деякі особливості.

1. Аналіз задач зводиться до встанов­лення (розпізнавання) виду задач, до

якого належить дана

2. Пошук розв'язування полягає у складанні на підставі загального правила (формули, тотожності) або загального положення (означення, те­ореми) програми – послідовності кроків розв'язування задач даного ви­ду. Звичайно, немає-необхідності цю програму формулювати в письмовій формі, достатньо її для себе намітити усно.

3. Саме розв'язання стандартної за­дачі полягає у застосуванні цієї за­гальної програми до умови даної за­дачі. Якщо деякі кроки програми розв'язування вимагають для свого виконання використання також інших програм, то стосовно них про­водяться ті самі операції (розпізна­вання виду задачі, складання програ­ми розв'язування і виконання розв'я­зування на основі цієї програми). Звідси походить, що для того щоб легко розв'язувати стандартні задачі (а вони є основними математичними задачами, оскільки всі інші зрештою зводяться до них), треба:

1) пам'ятати всі вивчені в курсі мате­матики загальні правила (форму­ли, тотожності) і загальні поло­ження (означення, теореми);

2) вміти розгортати згорнуті загальні правила, формули, тотожності, а також означення і теореми у про­грамі - послідовності кроків розв'язування задач відповідних видів.

У визначенні стандартних задач як основну ознаку цих задач вважають наявність в курсі математики таких загальних правил чи положень, які однозначно визначають програму розв’язання цих задач і виконання кожного кроку цієї програми.

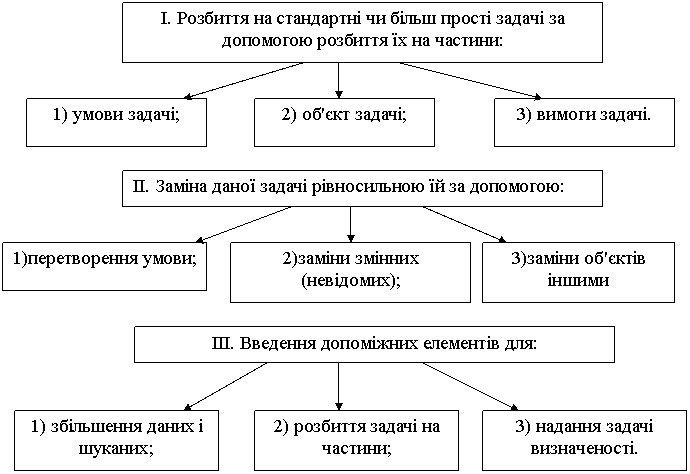
Звідси зрозуміло, що нестандартні задачі - це такі задачі, для яких в курсі математики немає загальних правил і положень, що визначають точну програму їх розв’язування.

Процес розв’язування будь-якої нестандартної задача складається у послідовному застосуванні двох основних операцій:

1. Зведення (шляхом перетворення або переформулювання) нестан­дартної задачі до іншої, їй еквіва­лентної, але уже стандартної задачі;

2. Розбиття нестандартної задачі на декілька стандартних підзадач.

В залежності від характеру нестан­дартної задачами використовуємо од­ну із цих операцій або обидві. При розв'язуванні більш складних задач ці операції доводиться застосовувати багаторазово.

МЕТОДИ РОЗВ'ЯЗАННЯ НЕСТАНДАРТНИХ ЗАДАЧ

Відомо, що будь-який урок — це складне педагогічне явище, ви­твір вчителя, на якому учні де­монструють свої знання, уміння та навички.

Чи цікаво дітям на уроці? Чи люблять вони вчитися?

На ці питання не можна відповіс­ти напевне. Іноді діти ідуть на урок із задоволенням, іноді без нього. Як зацікавити дітей? Як привернути їх увагу до свого предмету? Звичайно, за допо­могою того, що їм буде слухати найцікавіше, того, що вони бу­дуть робити із задоволенням.

Як донести матеріал до їх свідо­мості яскраво і красиво, щоб за­пам'яталось надовго і назавжди?

Іноді можна почути, що матема­тика складна, суха і нецікава на­ука. Людей, які люблять матема­тику, це вражає й ображає. Мате­матика сувора, але красива й гли­бока, як чиста криниця. А за­вдання — вчителя і полягає в то­му, щоб розкривати перед учня­ми її емоційний бік, чуйну і врод­ливу стать. Як краще цього до­могтися?

Красивими, цікавими уроками. Уроками, які пробуджують ціка­вість і працьовитість, фокусують увагу і зосередженість. Отже, не­стандартний урок. Він не вкла­дається в рамки виробленого і сформульованого дидактикою. На цьому уроці можна не дотри­муватись чітких етапів навчаль­ного процесу, методів, традицій­них видів роботи. Для такого уро­ку характерною є інформаційно-пізнавальна система навчання — оволодіння готовими знаннями, пошук нових форм викладу, роз­криття внутрішньої сутності явищ через гру, змагання або нетрадиційні форми роботи з дітьми, використовувати власні дидактичні матеріали, часто са­моробні і тим більше корисні для учнів.

Для прикладу наведу урок у 6 кла­сі з теми «Відсотки» під назвою «Бізнес-гейм».

Щоб наблизити математику до життя, щоб показати її різно­манітність застосування, цей урок було проведено у вигляді ділової гри.

Учнів класу було поділено на три команди, і весь урок вони працю­вали за груповим методом. Кож­на команда сиділа за окремим ве­ликим столом. Ідея уроку поляга­ла в тому, що учні — гості, які приїхали у місто «Відсоток», а вчитель — бізнесмен, мешка­нець цього міста, знайомить їх з ними і його мешканцями. Під час цієї мандрівки з учнями трап­ляються цікаві пригоди — вони витрачають і заробляють гроші, займаються бізнесом, а допома­гають їм у цьому відсотки. Урок краще проводити в кінці теми, щоб діти були знайомі з усіма ти­пами задач на відсотки. Цей урок вимагає гарної підготовки вчите­ля. Необхідно намалювати яск­раві плакати з написами об'єктів продажу, картки з задачами, при­нести гральний кубик і кашкети з написами «Бізнес-гейм». У про­веденні уроку вчителеві допома­гають учні цього класу — «праців­ники фірми». Учень начальник фінансів — буде вести банківські рахунки команд на одній з від­кидних дощок, троє менеджерів по одному біля кожного з трьох столів – для виплати коштів, зароблених учнем окремо та для то­го, щоб кидати гральний кубик.

Під час проведення цього уроку спостерігається велика зацікавленість учнів, вони активні, збуджені, працюють із задоволенням це можна пояснити, мабуть, тим, що учні відчувають себе у ролі бізнесменів, мають змогу заробити і витратити власний капі лат. Це урок – міні-модель сучасного життя, де без знань відсотків та їх застосування не обійтись. Тому ми бачимо і мотиваційний бік цього уроку. Під час підведення підсумків я відзначаю не тільки командну роботу певної групи учнів, але й індивідуальні відповіді.

Досвід роботи показує, що для поліпшення розуміння, закріплення та відтворення інформації доцільно проводити такі уроки як: урок-змагання; урок-вікторина, урок- “круглий стіл”; урок-гра та ін. Щоб зацікавленість учнів до вивчення математики не знижувалась, доречно систематично проводити ігри з використанням інтерактивних технологій.

Так у 9 класі практикую проведення уроків-змагання під час узагальнення і систематизації знань учнів з певної теми. Наприклад, урок узагальнення і систематизації знань за темою “Числові послідовності”. Клас поділено на три команди: “Трикутник”, “Квадрат”, “Коло”.

Актуалізація опорних знань учнів (міні-іспит) – у формі змагання між трьома командами. Кожна з команд задає другим командам по два питання; за правильну відповідь – плюс 1 бал, за неправильну – мінус 1 бал.

Математичне лото. Кожній з команд пропонується завдання, яке складається з дев’яти задач. До них додається стільки ж (квадратних) карток, на яких записані відповіді. Номер ставиться на тому боці картки, на якому записана відповідь. На зворотному боці картки написана частина висловлювання про математику.

Захист творчих робіт капіталами команд.

Підсумок уроку.

Така організація учбової діяльності на уроці дає можливість реалізувати принципи диференціації навчання, оскільки гарантує участь кожного учня на тому чи іншому етапі уроку. Так, учні з низьким рівнем навчальних здібностей можуть забезпечити команді бали на І етапі уроку, а учні з високими здібностями – виступи із захистом творчих робіт. Другий етап уроку – “поле діяльності” для учнів з середніми навчальними здібностями.

Позакласна робота з математики дуже важлива для пробудження в учнів інтересу до математики. Тому математичні вікторини, змагання, ігри, прес-конференції, вечори сприяють підвищенню математичної культури, розширюють і поглиблюють здобуті на уроках знання, показують застосування їх на практиці, розвивають мислення, математичні здібності, допомагають ввійти у світ наукових і технічних ідей.

Так при проведенні прес-конференції “Гранітна опора наук” учні 7-9 класів багато дізналися про значення математики в різних галузях людської діяльності. Така форма роботи сприяє розширенню кругозору учнів, розвиткові уміння самостійно й творчо працювати з навчальною, науково-популярною літературою, формуванню в дітей інтересу до математики, а також поглибленню знань.

Учням дуже подобається брати участь в іграх, правила яких максимально наближені до умов тих ігор, за якими вони мають можливість спостерігати з екранів телевізорів. Такими іграми є “Перший мільйон”, “Поле чудес”, “Слабка логіка” та інші.

Щоб розвинути творчі здібності учнів, поступово та систематично залучати до самостійної пізнавальної діяльності, щоб забезпечити співпрацю між учнями та учителем, традиційного уроку недостатньо.