Реферат: Умовний екстремум. Метод множників Лагранжа. Метод найменших квадратів

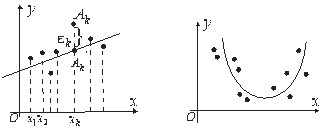
Рис.6.13 Рис.6.14

розглядуваний процес. Найпоширенішим методом розв’язання даної задачі є метод розв’язання даної задачі є метод найменших квадратів.

Нехай експериментальні точки групуються навколо прямої (див. рис. 6.13). Тоді

(6.97)

де і - параметри, які потрібно знайти.

Розглянемо експериментальну точку і точку з такою самою абсцисою, але яка лежить на прямій. Її координати . Різницю ординат цих точок

, (6.98)

що являє собою відхилення точки від прямої , назвемо похибкою.

Доберемо параметри і так, щоб сума квадратів похибок

(6.99)

була найменшою.

Підставимо в (6.99) вирази помилок (6.98), одержимо

(6.100)

Тут і відомі величини, а і - невідомі, які потрібно знайти. Для того щоб функція мала найменше значення, необхідно

виконати умови:

або

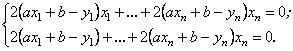
Перегрупувавши члени, подамо цю систему у вигляді

або

(6.101)

Ця система рівнянь називається нормальною системою методу найменших квадратів. Розв’язавши її, знаходимо і і підставляємо в емпіричну формулу .

Нехай тепер експериментальні точки розміщені поблизу деякої параболи (див. рис. 6.14). Тоді

(6.102)

Для знаходження і використаємо метод найменших квадратів. Відхилення за ординатою експериментальних точок від відповідних точок параболи

, (6.103)

Доберемо параметри і так, щоб сума квадратів похибок (6.104)

була найменшою. Для цього необхідно виконання умов

Обчисливши частинні похідні, маємо систему рівнянь

Перегрупувавши доданки в кожному із рівнянь, одержимо нормальну систему рівнянь методу найменших квадратів для параболічної залежності:

(6.105)

Із цієї системи знаходимо і і підставляємо їх в емпіричну формулу .