Реферат: Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних

Візьмемо довільну функцію , яка в околі деякої точки і в самій точці має похідні до -го порядку включно.

Тоді для такої функції можна побудувати многочлен

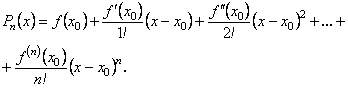(6.78)

Цей многочлен називається многочленом Тейлора для функції

Розглянемо таку різницю:

Оскільки залежить від то й залежить від

Тоді

або

(6.79)

Формула (6.79) називається формулою Тейлора для функції а функція - залишковим членом формули Тейлора.

Отже, формула Тейлора (6.79) відрізняється від формули Тейлора (6.77) для многочлена тим, що вона містить залишковий член Виразимо через похідну -го порядку від функції

Теорема. Якщо в деякому околі, наприклад, на відрізку точки має неперервні похідні до -го порядку включно, то залишковий член у формулі Тейлора можна записати у вигляді

(6.80)

де

Формула (6.79) записується тепер у вигляді

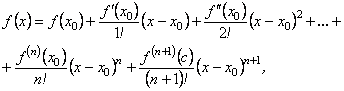(6.81)

і справедлива для будь-якого

Формула (6.81) називається формулою Тейлора із залишковим членом виду Лагранжа. Якщо в цій формулі покласти , то матимемо так звану формулу Маклорена

(6.82)

Враховуючи вирази для диференціалів різних порядків функції можна записати формулу (6.81) в диференціальній формі:

(6.83)

6.14.3. Формула Тейлора для функції двох змінних

Нехай функція має в околі точки неперервні частинні похідні до -го порядку включно. Формулу Тейлора зручно записати в диференціальній формі:

(6.84)

де

Аналогічний вигляд має формула Тейлора для функції більшого числа змінних.