Реферат: Теореми Ролля, Лагранжа, Коші. Правило Лопіталя. Формула Тейлора для функції однієї та двох змінних

Справді, нехай, наприклад, маємо невизначеність Інакше кажучи, нехай маємо функції і такі, що Тоді добуток можна зобразити у вигляді частки: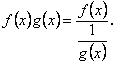

Отже, у правій частині ми маємо невизначеність виду

Якщо маємо невизначеність , тобто і то різницю можна записати:

отже, в правій частині маємо невизначеність виду

Якщо маємо степінь і тобто невизначеність виду , то її розкривають так.

Припускаючи, що , вираз має вигляд

У показнику при маємо невизначеність виду , яка (це було показано вище) зводиться до невизначеності . Аналогічно невизначеності розкриваються невизначеності , .

Приклади. Користуючись теоремами Лопіталя, знайти границі функцій:

1. 2. 3.

4. 5. 6.

7. 8.

Р о з в ’ я з о к. Перевіримо виконання умов теорем Лопіталя для першого прикладу. Для прикладів пропонуємо умови теорем перевірити самостійно.

1. Нехай . Розглядатимемо пів інтервал, де - довільне число. Тоді . Знаходимо похідні за будь-якого , а потім

.

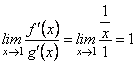Отже, виконуються всі три умови першої теореми Лопіталя. Тому

.

2. Маємо невизначеність виду . Використавши першу теорему Лопіталя, одержимо

.

3. Маємо невизначеність виду , тому використовуємо другу теорему Лопіталя:

.

4. Маємо невизначеність виду . Зводимо її до невизначеності . Для цього запишемо у вигляді

.

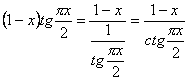Отже, дістали невизначеність . Тому

.

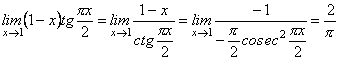5. Маємо невизначеність . Запишемо добуток

так: . Дістали невизначеність . Тому

Під знаком границі в правій частині останньої рівності знову маємо випадок, коли чисельник і знаменник прямують до , тобто маємо ту саму невизначеність . Застосувавши раз друге правило Лопіталя, дістаємо

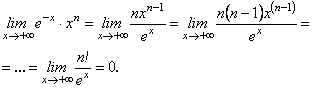
6. Маємо невизначеність . Тоді

Знайдемо границю показника:

тому

7.Маємо невизначеність виду . Запишемо даний вираз:

. Дістали невизначеність .

Отже,

.

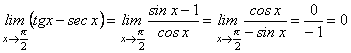8. Маємо невизначеність виду . Запишемо даний вираз:

.

Знайдемо границю показника:

.

Отже,

6.14. Формула Тейлора

6.14.1. Формула Тейлора для многочлена

Нехай задано многочлен

де - довільні дійсні числа, які називаються коефіцієнтами многочлена.

Виразимо коефіцієнти даного многочлена через значення многочлена та його похідні.

З цією метою будемо послідовно диференціювати многочлен. Матимемо

. . . . . . . . . . . . . . . . . . . .

Підставляючи в ці рівності , дістаємо

. . . . . . . . . .

Тоді многочлен набуде вигляду

(6.76)

Може трапитися, що многочлен буде записаний за степенями різниці , де - довільне дійсне число:

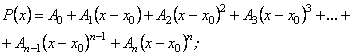
- дійсні числа. Тоді многочлен можна записати так:

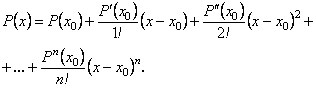(6.77)

Формулу (6.77) називають формулою Тейлора для многочлена.

6.14.2. Формула Тейлора для довільної функції