Реферат: Системи координат (декартова, полярна, циліндрична, сферична). Довжина і координати вектора. Векторний простір

Кожному сталому відповідає площина, паралельна площині . При зміні ці площини теж заповнюють весь простір .

Циліндрична система часто використовується у багатьох задачах математики, зокрема – в інтегральному численні.

7. Сферичні координати

Сферичними координатами є , а декартовими - і

. На рис.2.10 поєднано ці дві координатні системи. Тут набуває довільних невід’ємних значень, тобто .

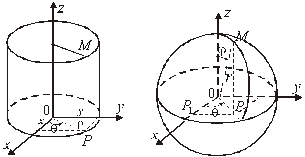
Рис.2.9 Рис.2.10

Кожному конкретному відповідає сфера радіуса з центром у початку координат. При зміні всі ці сфери заповнюють весь простір. Параметру відповідає півплощина, що проходить через вісь , а - кругові конуси, віссю яких є вісь . Тут мається на увазі двопорожнинний конус (рис.2.10). Тепер зрозуміло, що величина змінюється від 0 до , бо при такій зміні множина всіх конусів заповнює весь простір . Очевидно також, що .

Сферична система координат теж широко використовується в ряді галузей математики, зокрема при обчисленні потрійних інтегралів.

Зв’язок між сферичною і декартовою системою координат описується формулами

. (2.7)

Наприклад, перше з цих співвідношень доводиться так:

(із прямокутного трикутника ). Далі , що і треба було довести.

Інші співвідношення доводяться аналогічно.

9. Зміна системи координат

Розглянемо дві декартові системи координат: стару і нову Нехай довільна точка, координати якої в цих системах координат позначимо відповідно і Поставимо перед собою задачу виразити через

вважаючи відомими положення нової системи координат

відносно старої, тобто вважаючи відомими старі координати нового початку координат і координати нових базисних векторів в старому базисі, що складають матрицю переходу від базису

до базису

.

В матриці переходу стовпці – це координати нових базисних векторів

за старим базисом .

Радіус-вектори точки відносно точок і зв’язані рівністю

оскільки координати в базисі . Розкладемо кожен член даної рівності за базисом , маючи на увазі, що компоненти і дорівнюють координатам точок і які ми позначили відповідно через і Запишемо рівність в координатній формі

Рівності представляють закон перетворення координат точки при переході від однієї декартової системи координат до іншої.

Формули переходу від однієї декартової системи координат на площині до іншої можуть бути одержані із

Розглянемо частинний випадок, коли обидві системи координат – декартові прямокутні ( базиси - і Позначимо через кут між векторами і який відраховується в напрямку найкоротшого повороту від до Тоді (рис.2.11)

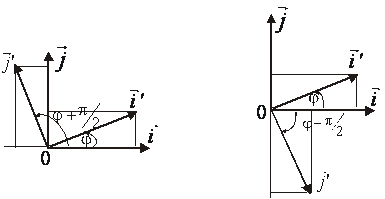
Рис.2.11а Рис.2.11б

В розкладі ставиться знак плюс (рис.2.11а), якщо найкоротший поворот від до направлений так само, як найкоротший поворот від до тобто якщо новий базис повернутий відносно старого на кут Знак мінус в розкладі ставиться в протилежному випадку, коли новий базис не може бути одержаний поворотом старого (рис.2.1б). Оскільки

одержимо

(2.8)

причому при повороті системи координат береться верхній знак.