Реферат: Системи координат (декартова, полярна, циліндрична, сферична). Довжина і координати вектора. Векторний простір

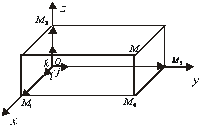
Рис.2.5

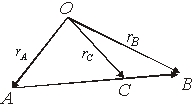
Якщо в системі координат задано вектор своїм початком і кінцем , то (рис.2. 6)

(2.2)

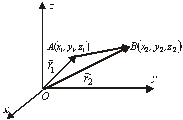
Рис.2.6

Цей факт доводиться досить легко.

НехайТоді з знаходимо

, що випливає безпосередньо з

правила віднімання векторів.

4. Поділ відрізка в заданому відношенні

Потрібно знайти координати точки, що ділить відрізок між точками і у відношенні (рис. 2.7).

Нехай і .

Тоді .

Звідси

Рис.2.7

Нехай координати точки дорівнюють відповідно . Тоді матимемо і

.

Оскільки два вектори рівні тоді і тільки тоді, коли рівні їх відповідні координати, то

(2.3)

Отже, координати точки знайдені.

Якщо точка середина відрізка то, очевидно, і з формули (2.3) одержимо координати середини відрізка

(2.4)

5. Полярні координати

Положення точки на площині можна визначити не тільки за допомогою прямокутної системи координат. Таку проблему можна розв’язати і так: виберемо на точку - полюс і проведемо півпряму

- полярну вісь (рис.2.8).

Положення точки на площині можна визначити віддаллю точки від полюса - полярним радіусом точки і кутом між і (полярним кутом ). Числа і називаються полярними координатами точки в полярній системі координат. Якщо , то точці буде відповідати лише одна пара чисел і , і навпаки. Для полюса (тобто точки ) , а - довільне число. Кут , як правило, відраховується від полярної осі проти годинникової стрілки (на рис. 2.8) це показано дуговою стрілкою).

Можна відмовитись від однозначності полярного кута при визначенні положення точки , враховуючи і кількість обертів, які здійснює полярний радіус, щоб його кінець потрапив в точку . Якщо кількість обертів позначити через , то полярний кут точки дорівнюватиме .

Відмовитись також можна і від обмеження на знак , щоб відрізнити точки і , що лежать на промені , вважаючи, що для точки полярний радіус , задля точки .

Далі будемо вважати, що , а . На рис. 2.8 зображені точки .

На рис.2.8 полярна система координат суміщена з прямокутною системою координат , причому полюс полярної

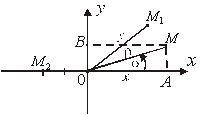
Рис.2.8 системи збігається з початком координат

прямокутної.

Точці відповідають координати полярної системи і координати прямокутної системи.

З прямокутного трикутника знаходимо

. (2.5)

Ці формули дають можливість перейти від полярних до прямокутних координат. З того самого трикутника знаходимо . Звідси

Ці формули дозволяють здійснити перехід від прямокутної до полярної системи координат.

6. Циліндрична система координат

Циліндричні координати є поєднанням полярних координат у площині і звичайної прямокутної (декартової) аплікати . Формули, що зв’язують ці дві системи координат, мають вигляд

(2.6)

де .

Тут кожному конкретному відповідає циліндрична поверхня. При зміні від 0 до такі циліндричні поверхні заповнюють весь простір . Твірні всіх цих циліндрів паралельні осі , а їх проекції на площину є кола з центром у початку координат (рис.2.9). Кожному конкретному відповідає півплощина, що проходить через вісь . При зміні від 0 до ця півплощина описує весь простір .