Реферат: Невласні інтеграли з безмежними границями та з необмеженою підінтегральною функцією

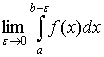(58)

її називають невласним інтегралом другого роду і позначають так:

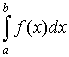(59)

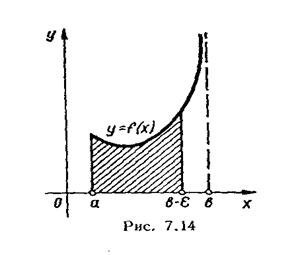
Отже, за означенням

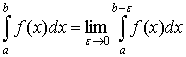
У цьому випадку кажуть, що інтеграл (59) існує або збігається. Якщо ж границя (58) нескінченна або не існує, то інтеграл (59) також називають невласним інтегралом, але розбіжним.

Аналогічно якщо х = — особлива точка (рис. 7.15), то невласний інтеграл визначається так:

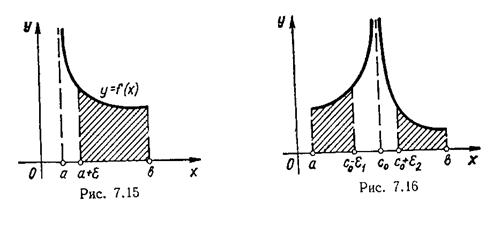
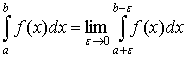
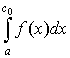Якщо f(x) необмежена в околі якої-небудь внутрішньої точки с0 (а; b), то за умови існування обох невласних інтегралів і 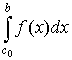за означенням покладають (рис. 7.16).

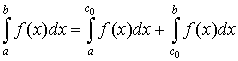
Нарешті, якщо а та b — особливі точки, то за умови існування обох невласних інтегралів 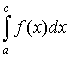і 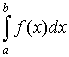за означенням покладають

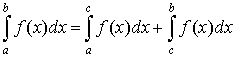
де с — довільна точка інтервалу (а; b).

Приклад

Обчислити невласні інтеграли:

а) 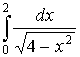; б)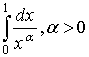

а)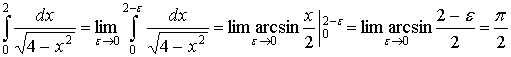

Отже, інтеграл а) збіжний.

б) Якщо ¹ 1, то

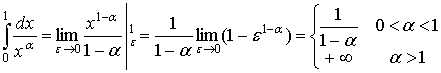
Якщо = 1, то

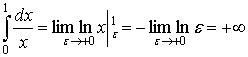
Таким чином, інтеграл б) збігається при 0 < < 1 і розбігається при ³ 1.

Бета-функція, або інтеграл Ейлера першого роду, визначається формулою

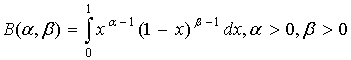(91)

Можна довести, що для всіх (0, +∞) і (0, +∞) інтег­рал (91) збігається. Варто зазначити, що відповідний невизначений інтеграл , згідно з теоремою Чебишева (п. 1.7), виражається через елементарні функції лише в окремих випадках. Отже, бета-функція не є елементарною.

Гамма-функцією, або інтегралом Ейлера другого роду, називається інтеграл

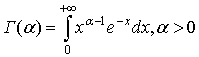(92)

Покажемо, що невласний інтеграл (92) при > 0 збігається. Маємо

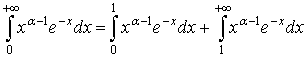
Перший інтеграл в правій частині цієї рівності збігається, бо

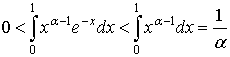
Другий інтеграл також збігається. Справді, якщо n — довільне натуральне число таке, що n > — 1, то

,

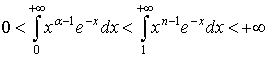в чому можна пересвідчитись, обчислюючи останній інтеграл части­нами і враховуючи, що

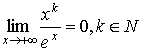
Отже, інтеграл (92) при > 0 збігається і визначає деяку функцію, яку і називають гамма-функцією Г().

Обчислимо значення Г() при а N. Якщо = 1, то

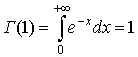(93)

Нехай n + 1 інтегруючи частинами, дістанемо

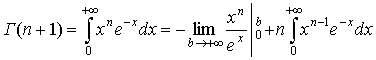
звідки

Г(n +1) = nГ(n) (94)

З рівностей (93) і (94) випливає, що nN:

Г(n +1) = n!

Таким чином, гамма-функція для цілих значень n N виражається через n!. Проте вона визначена і для нецілих додатних значень аргументу, тобто продовжує факторіальну функцію з дискретних значень аргументу на неперерв­ні. Гамма-функція не є елементарною функцією. Графік цієї функції зображено на рис. 7.35. Властивості гамма-функції досить добре ви­вчені і значення її протабульовані в багатьох довідниках, наприклад в [19].

Наводимо без доведення формулу Стірлінга для гамма-функції:

де > 0 і 0 < () < 1. Якщо в цій рівності покласти = n і помножити її на n, дістанемо

(95)

Бета- і гамма-функції пов'язані між собою співвідношенням

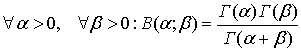(96)

Приклади

1. Знайти Г

Згідно з формулою (96), при = = маємо

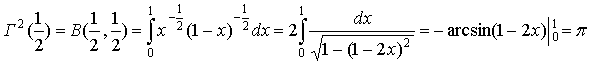
отже, Г=.

2. Обчислити інтеграл Ейлера — Пуассона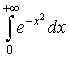

Враховуючи результат попереднього прикладу, дістанемо

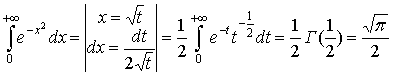
3. Виразити інтеграл 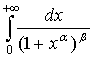через бета-функцію наближено при = 3, = .

Маємо

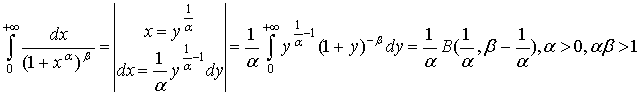
Зокрема, при = 3 і = згідно з формулою (96) дістанемо

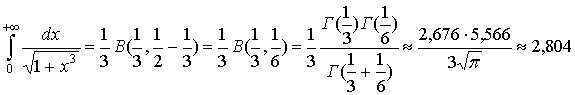
Завдання для самоконтролю

Які інтеграли називаються інтегралами, залежними від параметра?

Сформулювати теореми про неперервність, диференціювання та інтегрування Інтеграла, залежного від параметра.

3. Дати означення гамма-функції Г().

Довести, що Г(n +1) = n!, n N.

Дати означення бета-функції В(,). Як пов'язані між собою бета- та гам­ма-функції?

Довести, що

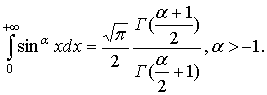
Вказівка. Скористатись підстановкою sin x = .