Реферат: Невласні інтеграли з безмежними границями та з необмеженою підінтегральною функцією
Згідно з теоремою існування визначеного інтеграла цей інтеграл існує, якщо виконані умови:
1) відрізок інтегрування [а, b] скінчений;
2) підінтегральна функція f(x) неперервна або обмежена і має скінченну кількість точок розриву. Якщо хоч би одна із умов не виконується, то визначений інтеграл називають невласним.
Якщо не виконується перша умова, тобто b = ∞ або а = ∞ або а = -∞ та b = ∞, то інтеграли називають невласними інтегралами з нескінченними межами.
Якщо не виконується лише друга умова, то підінтегральна функція f(x) має точки розриву другого роду на відрізку інтегрування [а, b]. В цьому випадку 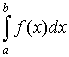 називають невласним інтегралом від розривної функції або від функції, необмеженої в точках відрізку інтегрування.
називають невласним інтегралом від розривної функції або від функції, необмеженої в точках відрізку інтегрування.
1. Невласні інтеграли з нескінченними межами інтегрування (невласні інтеграли першого роду).
Нехай функція f(х) визначена на проміжку [a; +∞) і інтегрована на будь-якому відрізку [а, b], де — ∞ < a < b < +∞. Тоді, якщо існує скінченна границя
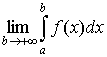 (51)
(51)
її називають невласним інтегралом першого роду і позначають так:
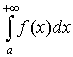 (52)
(52)
Таким чином, за означенням
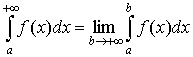 (53)
(53)
У цьому випадку інтеграл (52) називають збіжним, а підінтегральну функцію f(x) — інтегровною на проміжку [а; +∞).
Якщо ж границя (51) не існує або нескінченна, то інтеграл (52) називається також невласним, але розбіжним, а функція f(х) — неінтегровною на [a; +∞).
Аналогічно інтегралу (53) означається невласний інтеграл на проміжку (-∞; b]:
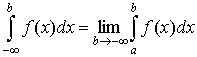 (54)
(54)
Невласний інтеграл з двома нескінченними межами визначається рівністю
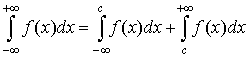 (55)
(55)
де с — довільне дійсне число. Отже, інтеграл зліва у формулі (55) існує або є збіжним лише тоді, коли є збіжними обидва інтеграли справа. Можна довести, що інтеграл, визначений формулою (55), не залежить від вибору числа с.
З наведених означень видно, що невласний інтеграл не є границею інтегральних сум, а є границею означеного інтеграла із змінною межею інтегрування.
Зауважимо, що коли функція f(x) неперервна і невід'ємна на проміжку [а; +∞) і коли інтеграл (53) збігається, то природно вважати, що він виражає площу необмеженої області (рис. 7.12).
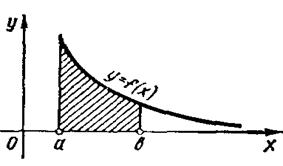
рис. 7.12
Приклад.
Обчислити невласний інтеграл або встановити його розбіжність:
а) 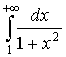 б)
б) 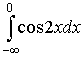
в) 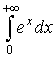 д)
д) 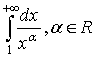
а) За формулою (53) маємо
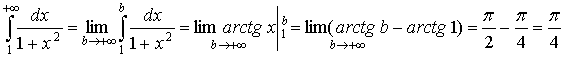
Отже інтеграл а) збігається.
б) 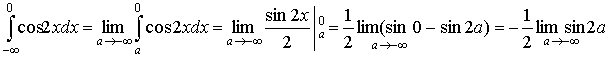
Оскільки ця границя не існує при а → -∞, то інтеграл б) розбіжний.
в) 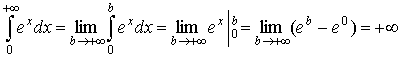
Отже інтеграл в) розбіжний,
г) Якщо ![]() = 1, то
= 1, то
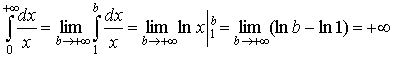
Якщо ![]() ≠ 1, то
≠ 1, то
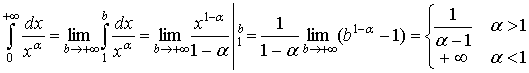
Отже інтеграл г) є збіжним при ![]() > 1 і розбіжним при
> 1 і розбіжним при ![]() ≤ 1.
≤ 1.
У розглянутих прикладах обчислення невласного інтеграла грунтувалося на його означенні. Проте у деяких випадках немає необхідності обчислювати інтеграл, а достатньо знати, збіжний він чи ні. Наводимо без доведення деякі ознаки збіжності.
Теорема 1. Якщо на проміжку [а; +∞) функції f(x) і g(x) неперервні і задовольняють умову 0 ≤ f(x) ≤ g(x), то із збіжності інтеграла
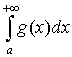 (56)
(56)
випливає збіжність інтеграла
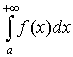 (57)
(57)
а із розбіжності інтеграла (57) випливав розбіжність інтеграла (56).
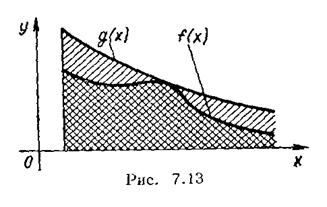
Наведена теорема має простий геометричний зміст (рис. 7.13); якщо площа більшої за розмірами необмеженої області є скінченне число, то площа меншої області є також скінченне число; якщо площа меншої області нескінченно велика величина, то площа більшої області є також нескінченно велика величина.
Приклад
Дослідити на збіжність інтеграли:
а) 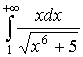 ;
; 
а) Оскільки ![]() :
:
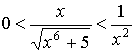
і інтеграл ![]() збігається, то за теоремою і заданий інтеграл також збігається.
збігається, то за теоремою і заданий інтеграл також збігається.
б) Цей інтеграл розбігається, бо ![]()
![]() :
:
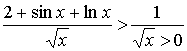
і інтеграл ![]() розбігається.
розбігається.
Теорема 2. Якщо існує границя
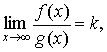
![]() ,
, ![]() ,
,
то інтеграли (56) і (57) або одночасно обидва збігаються, або одночасно розбігаються.
Ця ознака іноді виявляється зручнішою, ніж теорема 1, бо не потребує перевірки нерівності 0 £ f(x) ≤ g(х).
Приклад
Дослідити на збіжність інтеграл
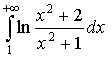
Оскільки інтеграл ![]() збігається і
збігається і
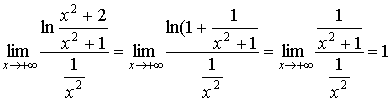
то заданий інтеграл також збігається.
В теоремах 1 і 2 розглядались невласні інтеграли від невід'ємних функцій. У випадку, коли підінтегральна функція є знакозмінною, справедлива така теорема.
Теорема 3. Якщо інтеграл 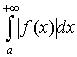 збігається, то збігається й інтеграл
збігається, то збігається й інтеграл 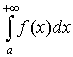 .
.
Приклад
Дослідити на збіжність інтеграл 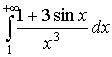 .
.
Тут підінтегральна функція знакозмінна. Оскільки
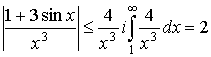
то заданий інтеграл збігається.
Слід зауважити, що із збіжності інтеграла 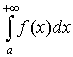 не випливає, взагалі кажучи, збіжність інтеграла
не випливає, взагалі кажучи, збіжність інтеграла 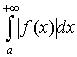 . Ця обставина виправдовує такі означення.
. Ця обставина виправдовує такі означення.
Якщо разом з інтегралом 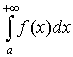 збігається й інтеграл
збігається й інтеграл 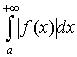 , то інтеграл
, то інтеграл 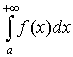 називають абсолютно збіжним, а функцію f(x) — абсолютно інтегровною на проміжку [а; +∞).
називають абсолютно збіжним, а функцію f(x) — абсолютно інтегровною на проміжку [а; +∞).
Якщо інтеграл 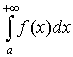 збігається, а інтеграл
збігається, а інтеграл 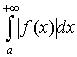 розбігається, то інтеграл
розбігається, то інтеграл 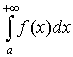 називають умовно (або неабсолютно) збіжним.
називають умовно (або неабсолютно) збіжним.
Тепер теорему 3 можна перефразувати так: абсолютно збіжний інтеграл збігається .
Отже, для знакозмінної функції викладені тут міркування дають змогу встановити лише абсолютну збіжність інтеграла. Якщо ж невласний інтеграл збігається умовно, то застосовують більш глибокі ознаки збіжності [II].
Приклад
Дослідити на збіжність інтеграл
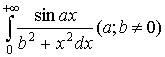
Оскільки
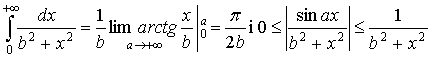
то за теоремою 3 інтеграл 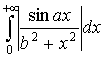 збігається.
збігається.
Отже, збігається, причому абсолютно, і заданий інтеграл, а функція f(x) =![]() на проміжку [0; +∞) є абсолютно інтегровною.
на проміжку [0; +∞) є абсолютно інтегровною.
2. Невласні інтеграли від необмежених функцій (невласні інтеграли другого роду).
Нехай функція f(x) визначена на проміжку [а, b). Точку х = b назвемо особливою точкою функції f(х), якщо f(x) → ∞ при х → b - 0 (рис. 7.14). Нехай функція f(x) інтегровна на відрізку [а; b — ![]() ] при довільному
] при довільному ![]() > 0 такому, що b -
> 0 такому, що b -![]() >
> ![]() ; тоді, якщо існує скінченна границя
; тоді, якщо існує скінченна границя