Реферат: Матриці. Загальна інформація

Системою m лінійних рівнянь з n невідомими х1 х2, ..., хn назива­ється система виду

( )

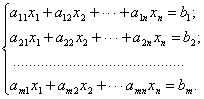Числа аij, і = 1, 2, .... m; j = 1, 2, ..., n біля невідомих назива­ються коефіцієнтами, а числа bi — вільними членами системи ( ).

Система рівнянь ( ) називається однорідною, якщо всі вільні чле­ни дорівнюють нулю, і неоднорідною, якщо хоч один з них відмінний від нуля.

Множина чисел а1, а2, ..., аn називається впорядкованою, якщо вка­зано порядок слідування цих чисел, тобто вказано, яке з них є пер­шим, яке другим, яке третім і т. д. Наприклад, якщо впорядкована трійка чисел, то в запису а, b, с число а вважається першим, b— дру­гим, с — третім, в запису b, а, с першим е число b, другим — число а і третім — число с.

Упорядкований набір n чисел () називається розв'яз­ком системи ( ), якщо при підстановці цих чисел замість невідомих х1, x2, ..., хn усі рівняння системи перетворюються в тотожності. Таку систему чисел називають також n-вимірним вектором, або точкою n-вимірного простору (див. п. 2.6, гл. 2).

Система рівнянь називається сумісною, якщо вона має хоча б один розв'язок, і несумісною, якщо вона не має жодного розв'язку.

Сумісна система називається визначеною, якщо вона має єдиний роз­в'язок, тобто існує тільки один набір n чисел , який пере­творює всі рівняння системи ( ) в тотожності.

Сумісна система називається невизначеною, якщо вона має більше, ніж один розв'язок.

Дві системи лінійних рівнянь називаються еквівалентними, якщо вони мають одну й ту ж множину розв'язків. Еквівалентні системи ді­стають, зокрема, внаслідок елементарних перетворень даної системи. Елементарні перетворення системи лінійних рівнянь відповідають еле­ментарним перетворенням матриці (п. 2.4) за умови, що вони викону­ються лише над рядками матриці.

Розв'язування систем лінійних рівнянь за формулами Крамера

Нехай задано систему двох лінійних рівнянь з двома невідомими х і у:

( )

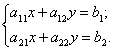Виконаємо такі елементарні перетворення системи ( ): спочатку помножимо перше рівняння на а22. Друге — на —а12, а потім складемо їх; після цього перше рівняння помножимо на а21, а друге — на —а11 і складемо їх. Дістанемо систему

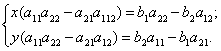
Систему ( ) можна записати за допомогою визначників:

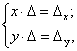
де

; ; .

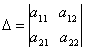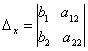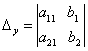Визначник , складений з коефіцієнтів системи ( ), називається визначником системи. Визначники у та х утворюються з визначника відповідно заміною стовпців при невідомих х та у вільними членами.

Використана література.

1. Беклемышев Д. В. Курс аналитической геометрии й линейной алгебры.— М. : Наука, 1987.— 320 с.

2. Бронштейн Й. Н., Семендяев К. А. Справочник по математике для инженеров й учащихся втузов.— М. : Наука, 1986.— 544 с.

3. Бурбаки Н. Очерки по истории математики.— М. : Изд-во иностр. лит., 1963.— 151 с.

4. Бугров Я. С., Никольский С. М. Елементи линейной алгебри й аналитической геометрии.— М, : Наука, 1983.— 228 с.

5. Бугров Я- С., Никольский С. М. Дифференциальное й интегральное нечисленне.— М. : Наука, 1988.— 431 с.

6. Бугров Я. С., Никольский С. М. Дифференциальные уравнения: Кратные интегралы. Ряди.— М. : Наука, 1989.— 464 с.

7. Самойленко А. М., Кривошея С. А., Перестюк Н. А. Дифференциальные уравне­ния.— К. : Вища шк., 1989.— 384 с.

8. Головина Л. Й. Линейная алгебра й некоторые ее приложения.— М. : Наука, 1985.— ,392 с.

9. Давидов М. О. Курс математичного аналізу: В 3 ч.— К. : Вища шк., 1990— 1992.— Ч. 1.— 383 с.; Ч. 2.— 366 с.; Ч. 3.— 359 с.