Реферат: Матриці. Загальна інформація
Основні означення
Прямокутна таблиця чисел aij = 1, 2, .... m; j= 1, 2, ..., n, складена з m рядків та n стовпців і записана у вигляді
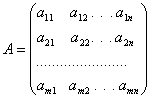або 
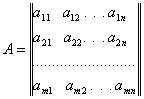
називається матрицею. Поняття матриці вперше ввели англійські математики У. Гамільтон і Д. Келі. Коротко матрицю позначають так:
або 
де aij — елементи матриці, причому індекс і в елементі aij означає номер рядка, aj— номер стовпця, на перетині яких стоїть даний елемент.
Добуток числа рядків m на число стовпців n називають розміром матриці і позначають m X n. Якщо хочуть вказати розмір m X n матриці А, то пишуть Аm
n.
Матриця, в якої число рядків дорівнює числу стовпців, називається квадратною. Кількість рядків (стовпців) квадратної матриці називається її порядком. Матриця, у якої всього один рядок, називається матрицею-рядком, а матриця, у якої всього один стовпець,— матрицею-стовпцем. Дві матриці Аmn=(aij) та Вmn= (bij) називаються рівними, якщо вони однакових розмірів і мають рівні відповідні елементи: аij = bij. Нульовою називається матриця, у якої всі елементи дорівнюють нулю. Позначається така матриця буквою О. Як і в визначниках (п. 1.1), в квадратних матрицях виділяють головну і побічну діагональ.
Квадратна матриця називається діагональною, якщо всі її елементи, крім тих, що знаходяться на головній діагоналі, дорівнюють нулю. Діагональна матриця, у якої кожен елемент головної діагоналі дорівнює одиниці, називається одиничною і позначається буквою Е. Наприклад, одинична матриця третього порядку має вигляд
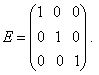
Будь-якій квадратній матриці
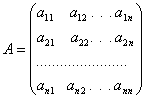
можна поставити у відповідність певне число, яке називається визначником (детермінантом) цієї матриці і позначається символом det А. За означенням
det A=
Наприклад, якщо
то det
Прямокутна матриця розміром т X п (п ф пі) визначника не має.
Дії над матрицями
1°. Операція додавання матриць вводиться тільки для матриць однакового розміру. Сумою С = А + В двох матриць Аmn — (aij) і Вmn = (bij) називається матриця Сmn= (cij)=(aij+bij). Наприклад,
2°. Добутком матриці Аmn = (aij) на число k (або числа k на матрицю Amn) називається матриця Вmn= (kaij). Наприклад,
3°. Різниця матриць А — В визначається як сума матриці А і матриці В, помноженої на — 1:
Справедливі такі властивості операцій:
а) А - В = В + А — комутативність відносно додавання матриць;
б) А + (В + С) — (А + В)+С — асоціативність відносно додавання матриць;
в) А + О — А; А — А = О — роль нульової матриці в діях над матрицями така, як і числа нуль в діях над числами;
г) 
(βA) = (β) А — асоціативність відносно множення чисел;
д) (А + В) = А +В — дистрибутивність множення на число відносно додавання матриць;
е) ( + β) А — А + βА — дистрибутивність множення на матрицю відносно додавання чисел.
4°. Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В.
Якщо ця умова не виконується, тобто матриці неузгоджені, то множення таких матриць неможливе.
З узгодженості матриці А з В не випливає, взагалі кажучи, узгодженість матриці В з А.
Квадратні матриці одного порядку взаємно узгоджені.
Добутком С = А В матриці Аmn — (аij) на матрицю Bnk=(bij) називається така матриця, у якої елемент сij дорівнює сумі добутків елементів j-го рядка матриці А на відповідні елементи четвертого стовпця матриці В:
cij=ai1b1j+ai2b2j+ … + ainbnj; C = Cmk = (cij),
i = 1, 2, …, m; j = 1, 2, …, k.
Це означення називають правилом множення рядка на стовпець. Наприклад, щоб визначити елемент с24, що стоїть в другому рядку і четвертому стовпці матриці С = АВ, потрібно знайти суму»добутків елементів другого рядка матриці А на відповідні елементи четвертого стовпця матриці В.
Для дій 1°—4° над матрицями виконуються такі властивості (за умови, що вказані операції мають зміст):
а) (АВ) С = А (ВС); б) (А) В = А (В) = (АВ);
в) (A + В) С = AС + BС; г) С (A + В) = СA + СB;
д) A • О = О • А = О; е) АЕ = ЕА = A; е) det (A5) = det А X det 5.
Обернена матриця
Нехай А — квадратна матриця. Матриця A-1 називається оберненою до матриці А, якщо виконується умова
А А-1 = А-1А = Е.
Квадратна матриця А називається виродженою, якщо det А=0, і невиродженою, якщо det А ≠0.
Теорема 3. Для існування оберненої матриці А-1 необхідно і достатньо, щоб матриця А була невиродженою.
О Необхідність. Нехай обернена матриця A-1 існує, тоді AA-1= Е. Застосовуючи правило знаходження визначника добутку двох матриць, маємо det A • det A-1 = 1, тому det А ≠ 0.
Достатність. Нехай det А ≠0, тоді матриця A має обернену матрицю А-1 причому
, ()
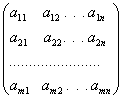де Аij — алгебраїчні доповнення елементів аij визначника матриці
()
Дійсно, добутки AA-1 і А-1 A матриць () і () дорівнюють матриці, у якої всі елементи головної діагоналі дорівнюють одиниці (за теоремою 1), а всі недіагональні елементи — нулю (за теоремою 2). Отже, А-1А = АА-1 = Е.
Покажемо, що А-1— єдина обернена матриця. Нехай А" — ще одна обернена матриця, тоді
А-1 = А-1Е = А-1(АА") = (А-1А)А" = ЕА" = А".
Ранг матриці
Нехай задано матрицю Аmхn= А. Виділимо в матриці А будь-які k рядків і стільки ж стовпців, де k — число, не більше чисел m і n, тобто k
min (m, n).
Визначник порядку k, складений з елементів, що стоять на перетині виділених рядків і стовпців, називається мінором k-го порядку матриці А.
Рангом r (А) матриці А називається найбільший з порядків ЇЇ мінор ів, відмінних від нуля.
Безпосередньо з означення випливає, що:
1) Ранг існує для будь-якої матриці Аmхn, причому
0r (A)min(m, n);
2) r (А) = 0 тоді і тільки тоді, коли А = 0;
3) для квадратної матриці n-го порядку ранг дорівнює n тоді і тільки тоді, коли матриця невироджена.
Ранг матриці можна знайти так. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то r = 0. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого порядку дорівнюють нулю, то r = 1. У випадку, коли є мінор другого порядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори порядку k дорівнюють нулю, або мінорів порядку k не існує, тоді r = k – 1.
Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов'язаний з обчисленням значного числа визначників. Простіший метод грунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме [1].
СИСТЕМИ ЛІНІЙНИХ РІВНЯНЬ
Основні означення