Реферат: Лінійні, однорідні та неоднорідні різницеві рівняння
Лінійні різницеві рівняння зі сталими коефіцієнтами
Означення. Лінійним різницевим рівнянням n-го порядку називається рівняння
(1)
де 
- сталі коефіцієнти. Якщо виразимо оператори різниць 
через оператор зсуву S, то можемо записати різницеве рівняння в рівнозначній формі
(2)
Число n називається порядком різницевого рівняння. Це рівняння можна також записати в операторній формі
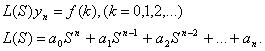(3)
Якщо 
, то різницеве рівняння називається однорідним, якщо , то рівняння називається неоднорідним.
Нагадаємо, що оператор зсуву S
(4)
Далі, замість слів “різницеве рівняння” будемо використовувати позначення РР. Для однозначного визначення розв’язків РР достатньо задати початкові умови
(5)
Означення. Розв’язком РР (2) називається послідовність 
(k=0, 1, 2,...), яка при підстановці її в РР (2) перетворює його в тотожність.
Приклад. Покажемо, що послідовність 
є розв’язком РР 
. Підставляючи значення , 
в РР, одержимо тотожність 
2. Однорідні різницеві рівняння
Наведемо деякі властивості розв’язків однорідного РР
(6)
Якщо РР (6) має частинні розв’язки 
, то воно має також розв’язок 
Якщо РР (6) має два розв’язки 
то воно має також розв’язок 
Звідси маємо, що РР має розв’язок:
Означення: Розв’язок РР (6) при 
.
(7)
називають загальним, якщо за рахунок вибору довільних сталих С1, С2,..., Сn можна задовольнити довільні початкові умови (6).
Якщо (7) загальне рішення РР (7), то система лінійних алгебраїчних алгебраїчних рівнянь 
Завжди має розв’язок відносно сталих С1, С2, ..., Сn.
Означення. Визначник
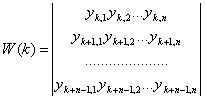(8)
називається визначником Вронського.
Замінюючи k на k+1 у визначнику (8), одержимо рівняння для значника Вронського 
Л. Ейлер запропонував загальний метод розв’язання РР (6). Розглянемо спочатку РР першого порядку 
.
З рівняння при k=0, 1, 2... одержимо рівняння
Виходячи з цього, РР (6) має частинний розв’язок.
Розв’язок 
обмежено при 
, прямує до нуля при 
, якщо 
необмежено зростає по модулю при 
Л. Ейлер запропонував шукати розв’язок РР (6) у вигляді 
Число μ називається мультиплікатором розв’язків РР (6).
Оскільки справедлива рівність 
, то для визначення мультиплікаторів одержимо алгебраїчні рівняння
або 
Це рівняння називається мультиплікаторним або характеристичним.
І. Якщо рівняння має n різних коренів 
, то загальний розв’язок РР (6) має вигляд 
Частинні розв’язки 
будуть лінійно незалежні, так як визначник Вронького
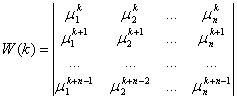
є визначником Вандермонда і відрізняється від нуля при 
.
Приклад. Знайдемо загальний розв’язок РР.
* Мультиплікаторне рівняння 
має розв’язок у1=2, у2=3. Тому РР має загальний розв’язок 
(k=0, 1, 2, ...).
Приклад. Знайдемо частинний розв’язок РР
з початковими умовами у0=0, у1=1.
* Мультиплікаторне рівняння 
має комплексні корені 
Загальний розв’язок в комплексній формі має вигляд
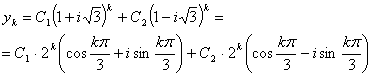
(k=0, 1, 2,...).
Цей розв’язок у дійсній формі має вигляд
Для визначення сталих С3, С4 одержимо систему лінійних алгебраїчних рівнянь
З цієї системи рівнянь знайдемо С3=0, С4=
Остаточно знаходимо частковий розв’язок 
що задовольняє задані початкові умови.
ІІ. Якщо рівняння має корінь μ1 кратності п1, то РР (6) має п1 лінійно незалежних часткових розв’язків
Наведемо теорему про загальний розв’язок РР (6).
Теорема 8.3. Якщо мультиплікаторне рівняння має корені 
кратності 
, то загальний розв’язок РР (6) одержимо у вигляді
Приклад. Знайдемо загальний розв’язок РР
Мультиплікаторне рівняння 
має трикратний корінь 
Тому загальний розв’язок має вигляд
3. Неоднорідне різницеве рівняння
Неоднорідне РР
(9)
завжди може бути зведене до підсумовування відомих функцій, якщо використовувати метод варіації довільних сталих.
Загальний розв’язок неоднорідного РР (9) є сумою частинного розв’язку неоднорідного РР та загального розв’язку однорідного РР.
Найбільш часто зустрічається РР
(10)
де Qq(k) – многочлен від k степеня q. Можна довести теорему.
Теорема 8.4. Якщо 
, то рівняння (10) має частковий розв’язок виду 
, де Rq(k) деякий многочлен від k степеня q.
Якщо 
є коренем кратності т рівняння , то РР (10) має частковий розв’язок виду 
.
Многочлен Rq(k) можна знайти методом невизначенних коефіцієнтів.