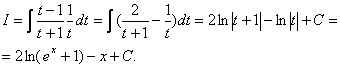Реферат: Інтегрування з допомогою заміни змінної. Інтегрування частинами

де неперервна функція з неперервною похідною, що має обернену функцію. Тоді і в цьому випадку має місце формула

(8.20)

Формулу (8.20) слід розуміти так, що після інтегрування в правій частині рівності замість буде підставлено його вираз через

Щоб довести рівність (8.20), потрібно довести, що похідні за від обох частин рівності рівні між собою:

Ми тут використали правило диференціювання оберненої функції.

Отже, похідні за від обох частин рівності (8.20) рівні, що й треба було довести.

Функцію потрібно вибирати так, щоби можна було обчислити інтеграл, що стоїть в правій частині рівності (8.20).

Фактично у п. 9.3.5 теж йшлося про заміну змінної, в чому можна безпосередньо переконатися .

Не можна дати універсальних замін змінних , які зводили б заданий інтеграл до простішого. Але для ряду випадків це можна здійснити. Доцільно, наприклад, в інтегралах, що містять під знаком інтеграла вирази вигляду

застосувати відповідно такі заміни змінних: або

або .

За подальшого вивчення методів інтегрування розглядатимуться інші заміни змінних .

Приклади .

1.. Підстановка зводить інтеграл до такого :

2.. Щоб позбутися експонент, доцільно скористатися такою заміною змінної .Тоді і інтеграл набере вигляду