Реферат: Інтегрування з допомогою заміни змінної. Інтегрування частинами

План

Інтегрування частинами

Інтегрування часток

Заміна змінної

1. Інтегрування частинами

Нехай і – диференційовані функції на

Тоді або

Звідси

(8.16)

Формула (8.16) називається формулою інтегрування частинами в невизначеному інтегралі.

Користуючись формулою (8.16), рекомендується обчислення інтегралів від таких функцій :

де –поліном , – раціональна функція . Описати всі можливі випадки застосування формули інтегрування частинами неможливо. Інтегруючи такі вирази, завжди виникає дилема : що взяти за, а що – за . Інтегруючи вирази вигляду , , після того як підінтегральна функція буде розписана за властивостями 40 і 50 , одержимо інтеграли вигляду , де - одна з функцій в яких слід за брати , бо, в протилежному випадку, інтеграл ускладнюватиметься за рахунок зростання степенів . В інтегралах , де - одна з функцій вигідно за брати . В інших випадках вибір здійснюється залежно від того, при якому з виборів легше знайти за , хоч це теж не є абсолютною істиною . Іноді доводиться експериментувати .

Інтегруючи вирази , доцільно за взяти . Знаходження із співвідношень теж здійснюється інтегрування частинами .

Для прикладу знайдемо

Приймаючи, а , знайдемо

Далі матимемо , тобто дістанемо інтеграл .

Знову, взявши , знайдемо . Отже , одержимо таку систему рівнянь відносно та :

Звідси

Приклад 1 .

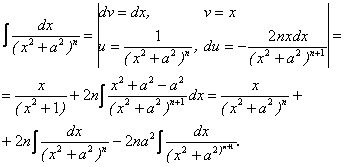
Позначивши ,

одержимо . Звідси

. (8.17)

Остання формула є рекурентною, тобто , знаючи , що , можна поступово знайти , де – ціле число,

більше за одиницю . Наприклад, при

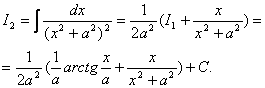
Звідси .

Приклад 2. .

Нехай Тоді

У новому інтегралі степінь величини понизився на одиницю, а це означає , що інтеграл став простішим , ніж був .

Знайдемо тепер . Маємо .

Звідси

Отже , на основі формули (8.16) одержимо

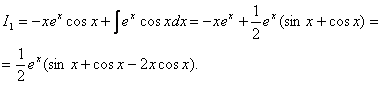
Враховуючи значення , знаходимо

Приклад 3.

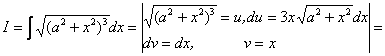
Із останньої рівності одержимо

Обчислимо тепер

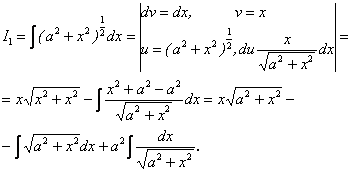
Звідси .

Остаточно з урахуванням , матимемо

Останній приклад показує, що часто інтегрування частинами приводить до мети скоріше в тих випадках, де, як це здавалось би, доцільніше застосувати інші методи . У цьому можна переконатися, спробувавши знайти первісну для функції , застосувавши наприклад , заміну змінної за формулою , про що мова буде іти пізніше.