Реферат: Інтегрування виразів, що містять тригонометричні функції. Приклади первісних, що не є елементарними функціями

(8.27)

Тоді

Піднісши до степеня і розкриваючи дужки, одержимо інтеграли, що містять в парних і непарних степенях. Інтеграли з непарними степенями обчислюються, як показано у випадку б). Парні показники степенів знову понижуємо за формулами (9.13). Продовжуючи так, дійдемо до інтегралів які легко обчислюються.

Якщо хоча б один з показників від’ємний, то необхідно робити підстановку (або ).

Інтеграли вигляду можна

проінтегрувати, застосовуючи формулу Муавра. Маємо:

(8.28)

Звідси

Далі обчислимо:

Аналогічно

Тепер уже інтегрування двох інтегралів здійснюється легко для будь-яких скінчених цілих .

е) Усі інтеграли вигляду

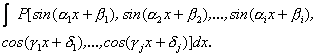
можуть бути представлені в замкненому вигляді, якщо функція є цілою раціональною функцією відносно синусів і косинусів величин, що стоять під знаком функції, а всі константи є дійсними числами.

Оскільки ціла раціональна функція будується лише на основі дій додавання, віднімання і множення ( зокрема піднесення до цілого додатного степеня ) , то кожний добуток двох множників можна подати у вигляді суми двох доданків на основі формул

(8.29)

Застосовуючи формули (8.29) послідовно до кожного члена, що є добутком кількох множників, функцію можна подати як лінійну комбінацію синусів і косинусів, аргументи яких є лінійними функціями . Кожна така лінійна комбінація інтегрується елементарно.

Приклад.

є) Усі інтеграли виглядів де є довільними дійсними константами, а – довільний поліном, інтегруються у замкненому вигляді.

Цей висновок випливає з п.8.3.8.

ж) Інтеграли вигляду за допомогою підстановки зводяться до інтегралів від біномінальних диференціалів , які вже були розглянуті в п.8.3.8 є). Там також було з’ясовано, в яких випадках інтеграл від біномінального диференціала інтегрується в замкненому вигляді. Отже, інтеграл виражається через елементарні функції, якщо 1) - ціле число; 2)- ціле число; 3)- ціле число.