Реферат: Інтегрування виразів, що містять тригонометричні функції. Приклади первісних, що не є елементарними функціями
План
Інтегрування виразів, що містять тригонометричні функції
Інтеграли вигляду ![]()
Інтеграли вигляду ![]()
Інтеграли вигляду ![]()
· Інтеграли вигляду ![]()
Інтеграли вигляду![]() (
(![]() - ціле, додатне число)
- ціле, додатне число)
Інтеграли вигляду ![]()
8.3.9. Інтегрування трансцендентних функцій
а) Усі інтеграли вигляду ![]() інтегруються в замкненому вигляді. Тут
інтегруються в замкненому вигляді. Тут ![]() - символ раціональної функції. Справді, підстановка
- символ раціональної функції. Справді, підстановка ![]() зводить цей інтеграл до вигляду
зводить цей інтеграл до вигляду ![]()
Приклад. ![]() За допомогою заміни
За допомогою заміни ![]() інтеграл перетворюється в такий :
інтеграл перетворюється в такий :
![]()
б) ![]() Як уже зазначалося, інтеграли
Як уже зазначалося, інтеграли ![]() зводяться до розглядуваного. Тому інтеграл
зводяться до розглядуваного. Тому інтеграл ![]() нас цікавить не тільки сам по собі, а й у зв’язку з тим, що й інші інтеграли зводяться до нього.
нас цікавить не тільки сам по собі, а й у зв’язку з тим, що й інші інтеграли зводяться до нього.
Усі інтеграли типу ![]() інтегруються в замкненому вигляді. Підстановка
інтегруються в замкненому вигляді. Підстановка ![]() перетворює інтеграл у такий:
перетворює інтеграл у такий:![]() тобто до інтеграла, розглянутого в п.9.8.
тобто до інтеграла, розглянутого в п.9.8.
Ймовірно, що способи інтегрування заданого інтеграла в розумінні більшої або меншої трудності залежатимуть від характеру функції ![]() : парна чи непарна вона за змінною
: парна чи непарна вона за змінною ![]() або
або ![]() , або і
, або і ![]() і
і ![]() , або, можливо, і не володіє цими властивостями. Нехай
, або, можливо, і не володіє цими властивостями. Нехай
![]() Очевидно, що в цьому випадку її можна подати
Очевидно, що в цьому випадку її можна подати
у формі ![]()
Якщо ![]() то
то

Тому

Звідси випливає така підстановка:
![]() ,
,
тобто ![]() - раціональна функція
- раціональна функція ![]() .
.
Отже, якщо в разі заміни ![]() на
на ![]() підінтегральна функція змінює знак, то доцільно є підстановка
підінтегральна функція змінює знак, то доцільно є підстановка ![]() .
.
Цілком аналогічно, якщо в разі заміни ![]() на
на
![]() то доцільною є
то доцільною є
підстановка ![]() .
.
Розглянемо тепер випадок ![]() тобто функція
тобто функція![]() є парною як за
є парною як за ![]() , так і за
, так і за ![]() . Очевидно, що
. Очевидно, що ![]() .Якщо тепер знаки
.Якщо тепер знаки ![]() i
i ![]() замінити на протилежні, то
замінити на протилежні, то![]() , тобто
, тобто ![]() є парною за
є парною за ![]() , тому
, тому
![]() . Вважаючи, що
. Вважаючи, що ![]() , одержимо
, одержимо
![]()
![]()
Підстановка ![]() зведе інтеграл до вигляду
зведе інтеграл до вигляду ![]()
Отже, у випадку ![]() доцільною є заміна змінної
доцільною є заміна змінної ![]() .
.
Оскільки  ,
,  , (8.26)
, (8.26)
то 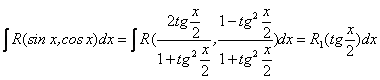 ,
,
тобто підстановка ![]() перетворить інтеграл до вигляду
перетворить інтеграл до вигляду
![]() .
.
Якщо ![]() не задовольняє жодну із розглянутих умов, то
не задовольняє жодну із розглянутих умов, то ![]() інтегрується за допомогою підстановки
інтегрується за допомогою підстановки ![]() . Практично інтегруючи функцію
. Практично інтегруючи функцію ![]() перш за все варто встановити, чи задовольняє вона хоча б одну з умов
перш за все варто встановити, чи задовольняє вона хоча б одну з умов ![]()
![]()
чи ні. Лише тоді, коли вона не задовольняє жодну, доцільно використати заміну ![]() , яку називають універсальною.
, яку називають універсальною.
Приклад. 1. ![]()
Оскільки в разі заміни ![]() на
на ![]() і
і ![]() на
на ![]() підінтегральна функція не змінює знака, то підстановка
підінтегральна функція не змінює знака, то підстановка ![]() зведе інтеграл до вигляду
зведе інтеграл до вигляду

Приклад 2. ![]() .
.
Цей інтеграл не задовольняє жодної з указаних умов. Тому слід використати підстановку ![]() , яка зведе інтеграл до вигляду
, яка зведе інтеграл до вигляду
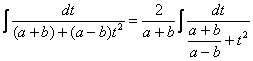 .
.
Якщо ![]() , то
, то
![]() .
.
Якщо ![]() , то
, то 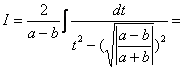

При 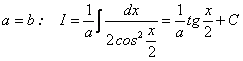 .
.
При 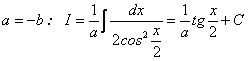 .
.
Приклад 3. ![]() .
.
Підстановка ![]() . З її допомогою інтеграл перетвориться в
. З її допомогою інтеграл перетвориться в
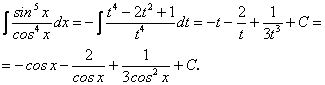 .
.
в) Усі інтеграли вигляду
![]() де
де ![]() - раціональна функція, інтегруються в замкненому вигляді. Цей висновок випливає з п.9.4.
- раціональна функція, інтегруються в замкненому вигляді. Цей висновок випливає з п.9.4.
г) Інтеграли вигляду ![]()
![]() (
(![]() - ціле, додатне число) можна проінтегрувати відповідно за допомогою підстановок
- ціле, додатне число) можна проінтегрувати відповідно за допомогою підстановок ![]()
В результаті матимемо
![]()
Аналогічно обчислюється і другий інтеграл.
д) Інтеграли вигляду ![]() де
де![]() - цілі невід’ємні числа, обчислюються, використовуючи формули тригонометрії для пониження степеня:
- цілі невід’ємні числа, обчислюються, використовуючи формули тригонометрії для пониження степеня: