Реферат: Інтегрування раціональних функцій

Розглянемо конкретний приклад розкладу на прості дроби правильного раціонального дробу

в якому знаменник уже розкладений на множники. Коренями знаменника є однократний корінь 1, двократний корінь 2, двократна пара комплексно спряжених коренів (корені рівняння ), однократна пара комплексно спряжених коренів (корені рівняння ).

Отже , заданий дріб може бути поданий як

де - невідомі коефіцієнти , які треба обчислити, виходячи з того, що написана рівність є тотожністю. Її можна записати , звільнившись від знаменників:

Якщо прирівняємо коефіцієнти за однакових степенів у правій і лівій частинах одержаної тотожності після того, як у правій частині будуть виконані дії і згруповані члени з однаковими степенями , то одержимо систему дев’яти лінійних рівнянь із дев’ятьма невідомими відносно невідомих коефіцієнтів, які й знайдемо із вказаної системи рівнянь. У курсі алгебри доведено, що необхідна система рівнянь для визначення невідомих коефіцієнтів завжди має єдиний розв’язок .

Але можна зробити інакше : в написану тотожність замість по черзі підставити корені знаменника дробу ( хоч можна замість підставляти довільні числа.). В результаті одержимо шість невідомих коефіцієнтів. Отже, залишиться знайти ще три коефіцієнти .

При , а при , при матимемо , Звідси дістаємо систему рівнянь з якої знаходимо . При аналогічно знайдемо . Отже, залишилися невідомими . Їх можна знайти, підставляючи в тотожність замість , наприклад, . Із врахуванням значень з системи трьох лінійних рівнянь з трьома невідомими можна визначити .

Якщо безпосередньо скористатись тотожністю і зрівняти коефіцієнти за однакових степенів у правій і лівій частинах, то одержимо таку систему рівнянь: Після визначення всіх невідомих коефіцієнтів цієї системи рівнянь вже легко буде проінтегрувати заданий дріб, користуючись формулами простих раціональних дробів (п. 9.7.1).

Якщо знаменник раціонального дробу має лише прості корені (дійсні або комплексні), то невідомі коефіцієнти найпростіше можна знайти підстановкою коренів знаменника в тотожність (такого самого типу, що і у попередньому прикладі) замість .

Приклад. Обчислити інтеграл:

Р о з в ‘ я з о к. Розкладемо знаменник на множники

Тоді розкладемо підінтегральний дріб на прості дроби:

=

Одержимо

і

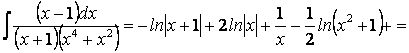
Виділення раціональної частини інтеграла.

Метод Остроградського

Розглянемо правильний раціональний дріб . При розкладі його на прості дроби одержимо таку суму простих дробів:

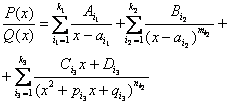(8.22)

Перша група доданків у цій сумі в результаті інтегрування дає

,

тобто ірраціональний вираз. Друга група доданків, якщо її проінтегрувати, буде такою:

.

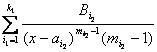Третя група доданків після інтегрування:

.

Використовуючи рекурентну формулу, зведеться до суми правильного раціонального дробу і з деяким числовим множником . Якщо (8.22) проінтегрувати і додати всі дроби раціональної частини інтеграла, одержимо правильний дріб вигляду , де

, а - поліном, степінь якого буде меншим, ніж степінь полінома в знаменнику. Тому

, (8.23)

де - теж раціональний дріб, усі множники знаменника якого

або лінійні, або квадратні в першому степені, або їх комбінації, причому .

Із (8.23) знаходимо

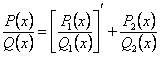(8.24)

Тут поліноми і - невідомі, степені їх треба брати на одиницю меншими, ніж степені в знаменнику, при цьому їх треба записувати з невизначеними коефіцієнтами, які знаходять так само, як і в разі розкладу раціонального дробу на прості дроби. Але перш, ніж звільнитися від дробів у (8.24), треба скоротити дріб, одержаний від диференціювання, на спільні множники чисельника і знаменника, якщо у знаменнику були степені множників більші за одиницю. У всіх випадках після диференціювання знаменник дробу повинен дорівнювати .

Приклад.

.

Р о з в ‘ я з о к. Підінтегральну функцію, користуючись формулою (8.24), подамо у вигляді

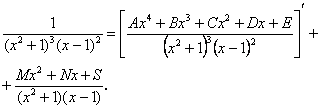
де - невідомі числа.

Розглянемо дріб ,

де .

Тоді

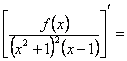
Тут здійснено скорочення на . Якщо цього не зробити, то далі виникнуть труднощі, викликані тим, що отримаємо систему рівнянь, в якій буде більше рівнянь, ніж невідомих коефіцієнтів.

Для визначення невідомих коефіцієнтів одержимо таку систему рівнянь: