Реферат: Інтегрування раціональних функцій

План

Інтегрування раціональних функцій

Прості раціональні дроби

Неправильні раціональні дроби

Інтегрування правильного раціонального дробу. Формула Остроградського

1. Інтегрування раціональних дробів

Прості раціональні дроби

Простими раціональними дробами називаються такі чотири види дробів :

,

де –дійсні числа ; – ціле число , тобто не розкладається на лінійні множники в множині дійсних чисел .

Розглянемо тепер інтеграли від цих дробів :

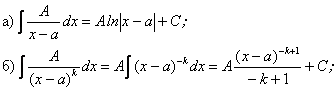
в) ;

г)

Цей дріб може бути зведений до іншого вигляду виділенням у знаменнику повного квадрата, а в чисельнику похідної від знаменника, помноженої на деяку константу .

Маємо

.

Отже,

Якщо позначити

, то одержимо

то одержимо

Тому

Щоб одержати кінцевий результат, досить повернутися до змінної і замінити та їх значеннями.

г) Четвертий тип простого дробу за допомогою тих самих перетворень, що й третій, зведеться до вигляду

Тому

Останній же інтеграл може бути про інтегрований за рекурентною формулою (9.3).

Неправильні раціональні дроби

Раціональний дріб має вигляд , де і - поліноми за степенів, відповідно і . Якщо степінь полінома не менший за степінь полінома , тобто то дріб називається неправильним. Якщо ж степінь полінома менший, ніж степінь полінома , то дріб називається правильним. Усякий неправильний дріб може бути поданий сумою деякого полінома (ціла частина дробу) степеня і правильного дробу. Цілу частину неправильного дробу можна виділити прямим діленням чисельника на знаменник. Ділення це продовжується доти, поки остача від ділення (це буде деякий поліном або просто число) матиме менший степінь, ніж степінь полінома, що є дільником.

Приклад 1. Виділити цілу частину дробу

Оскільки і , то дріб неправильний. Ми можемо безпосередньо виділити цілу частину, додавши і віднявши в чисельнику 8:

Приклад 2. Виділити цілу частину дробу

Отже,

.

Інтегрування правильного раціонального дробу

Якщо дріб неправильний, то розклавши його на суму цілої частину і правильного раціонального дробу, будемо інтеграл розглядати як суму інтегралів. Інтегрування цілої частини (полінома степеня ) не представляє ніяких труднощів. Тому розглянемо саме інтегрування правильних раціональних дробів.

Саме визначення простих дробів вказує на те, що перш ніж розкладати правильний дріб на прості, треба знаменник правильного дробу розкласти на прості множники. Під простими множниками розумітимемо множники вигляду і

Нехай знаменник правильного дробу має вигляд

,

де всі - дійсні числа. Тут коефіцієнт при вважаємо таким, що дорівнює одиниці, яка не зменшує загальності міркувань, бо у випадку наявності при коефіцієнта завжди можна чисельник і знаменник дробу поділити на Згідно з основною теоремою алгебри поліном – го степеня має рівно коренів на множині комплексних чисел.

З алгебри відомо також, що коли поліном з дійсними коефіцієнтами має комплексний корінь вигляду , то він має і спряжений йому корінь , тобто комплексні корені входять у поліном комплексно спряженими парами.

Згідно з теоремою Вієта поліном розкладається на множники вигляду , де - корені полінома, тобто

Нехай і - комплексно спряжені корені. Тоді їм відповідатиме в розкладі два множники і . Їх добуток

Отже, кожній спряженій парі комплексних коренів відповідає множник вигляду . Серед коренів полінома можуть виявитися кратні. Якщо врахувати це, то розклад полінома на множники запишеться так:

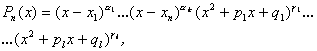(8.21)

де - кратності дійсних коренів, - кратності пар комплексно спряжених коренів.

Нехай правильний дріб має вигляд , де і – степені поліномів і і розкладається на множники так, як це показано в (8.21). У курсі алгебри доводиться, що кожному простому дійсному кореню відповідає простий дріб , а - кратному відповідає сума простих дробів:

Кожній парі комплексно спряжених коренів відповідає простий дріб вигляду , де кожній - кратній парі комплексно спряжених коренів відповідає сума простих дробів: