Реферат: Інтегрування і пониження порядку деяких диференціальних рівнянь з вищими похідними

Звідки.

Отже маємо

Прийшовши до отсанньої рівності ми отримаємо а)

Пониження порядку ДР які не містять незалежної змінної.

Ці ДР мають вигляд (4.59)

і його можна понизити на один порядок заміною

При цьому стане незалежною зміною, а - функцією

Обчислюємо

…..

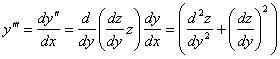
і остаточно прийдемо до ДР порядку

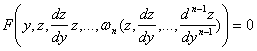
Якщо - розвязок ДР (4.60) то

Інтегруємо ДР (4.61) і знайдемо загальний інтеграл.

Особливі зорвязки можуть появлятися при інтегруванні ДР (4.61). При переході до ДР (4.60) ми можимо загубити розвязки .

Для їх знаходження необхідно розвявати р-ня .

Якщо - розвязок однорідного р-ня, то - розвязок ДР (4.59)

Пр. 4.6 Розвязати р-ня

Вводимо змінну , ,

,

звідки , отже, ,

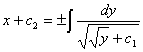
-загальний інтергал рівняння.

4. Однорідні ДР відносно шуканої ф-ї та її похідних.

Так називаються ДР вигляду в якому являється однорідною ф-єю відносно , тобто маємо

Шляхом заміни ДР (4.62) можна понизити на один порядок.

Обчислюємо

Тому ДР (4.62) прийме вигляд

(4.63)

Скорочуючи на ( при може бути розвязком ДР (4.62)), перейдемо до ДР порядку .

Якщо – загальний розвязок останнього ДР, то

звідки (4.64) – загальний розвязок ДР (4.62). Розвязок міститься в формулі (4.64) при .

Пр 4.7 Знайти загальний розвязок ДР

Це ДР являється однорідним відносно шуканої ф-ї і її похідних, тому .

Маємо ДР Бернулі – .

Інтегруючи отрімаємо , Звідки . Наше ДР має розвязок який не міститься в знайденому загальному інтергалі.

ДР, ліва частина якого є точна похідна.

Припустимо, що ДР (4.62), його ліва частина, є точна похідна по від деякої ф-ї , тобто ,

тоді ДР (4.62) має перший інтерграл (4.64) так, що яого порядок можна понизити на одиницю.

Пр 4.8 Розвязати ДР

Маємо , ,, – загальний інтеграл. Якщо ліва частина ДР (4.62) не являється точною похідною, то в деяких випадках можна знайти ф-ю , після домноження на яку р-ня (4.62), його ліва частина буде точною похідною. Ця ф-я називається інтергрувальним множником. Якщо ми знаємо ф-ю , то можна знайти не тільки перший інтеграл, а й особливі розвязки, які знаходяться з р-ня

Пр 4.9 Знайти загальний розвязок ДР .

Візьмемо , тоді .

При цьому , - розвязки нашого ДР.

Маємо .

- перший інтерал.

, загальний інтергал.

Особливих розвязків немає, так як ДР приводіть до розвязків , які містяться в загальному.