Реферат: Інтегрування і пониження порядку деяких диференціальних рівнянь з вищими похідними
ДР що містять n-ту похідну від шуканої функції і незалежну змінну.
а) Розглянемо ДР 
(4.38)
Так як 
, то
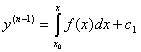
Аналогічно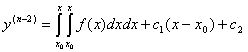 
, …..,
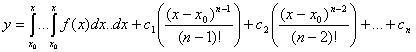(4.39)
Остання формула дає розвязок загальний в області
Формулу (4.39) легко використати для знаходження розвязків задачі Коші з начальними умовами
(4.40)
Цей розвязок представляється в вігляді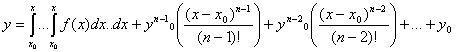 
(4.41)
Ф-я
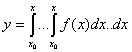
являється частиним розвязком ДР (4.38) з початковими умовами
яким відповідають константи 
Для обчислення використовують ф-лу Коші
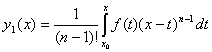(4.42)
Дійсно інтеграл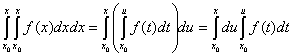 
можна розглядати як повторний інтеграл в заштрихованій області (мал. 1).
Міняючи порядок інтегрування, отримаємо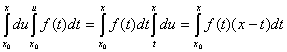 
Аналогічно обчислюємо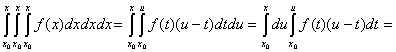 
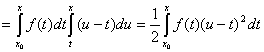.. і. т. д.
Приходимо до ф-ли (4.42)
Таким чином розвязок (4.41) записується у вигляді 
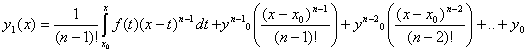
Загальний розвязок ДР (4.38) можна також записати через невизначений інтеграл
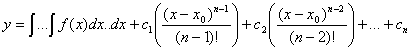
Пр. 4.4 Розвязати рівняння 
Послідовно знаходимо 
, 
б) Розглянемо випадок 
(4.43)
в якому співвіднощення (4.43) не можна розвязати відносно 
в елементарних ф-ях, або вирази для будуть досить складними.
Припустимо, що ДР (4.43) допускає параметризацію (4.44)
(4.44),
де 
та 
такі, що 
Проводимо обчислення 
, 
Аналогічно обчислюємо 
Остаточно маємо
(4.45) -загальний зорвязок в параметричній формі.
Відмітимо два випадки, в яких ДР (4.43) легко параметрмзується
I.
(4.46)
(частинні випадки 
)
II. 
(4.47), де 
і 
-однорідні ф-ї відповідного
виміру 
і 
.
Покладемо 
(4.48)
і розвяжемо р-ня (4.47) відносно 
через 
: 
Піставляючи в (4.48), отримаємо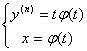 
(4.49)
Дальше вищеотриманим способом знаходимо загальний розвязок в параметричній формі.
Пр. 4.5 Розвязати р-ня 
Зробимо заміну 
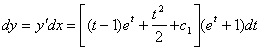остаточно маємо
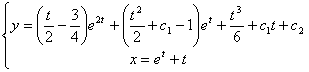
Інтегрування ДР, які не містять шуканої ф-ї та 
похідної.
Розглянемо ДР 
(4.50), в якому є 
.
Введемо нову змінну 
(4.51)
отримаємо 
(4.52)
тобто ми понизили порядок ДР (4.50) на одиниць.
Припустимо, що ми розвязали ДР (4.52) і визначили 
(4.53)
Тоді р-ня 
(4.54)
інтегруємо і отримаємо загальний розвязок 
(4.55)
Якщо замість загального розвязку (4.53) можна знайти загальний інтеграл 
(4.54)
то отримаємо ДР 
типу (4.43)
Розглянемо два частичних випадка відносно ДР (4.50) :
а) ДР вигляду 
якщо ДР (4.51) можна розвязати відносно :
(4.52)
то поклавши 
перейдемо до р-ня 
Якщо 
- загальний розвязок останнього р-ня, то остотаточно маємо р-ня вигляду (4.38) 
Припустимо, що ДР (4.51) не можна записати в вигляді (4.52), але воно допускає параметризацію 
(4.53)
то з співвідношення 
знаходимо 
Звідки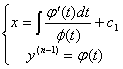 
(4.54)
ДР (4.54) вигляду (4.44) і розвязки можна отримати в параметричній формі.
б) ДР вигляду 
(4.55)
Нехай ДР (4.55) можно розвязати відносно
(4.56)
Позначимо
і перейдемо до ДР 
(4.57)
Домножимо (4.57) на 
: 
Звідки 
. Отже 
з якого визначимо
.
Останнє ДР є р-ням з відокремлюваними змінними.
Знайшовши з нього
ми остаточно переходимо до ДР вигляду (4.38).
(4.58)
Припустимо, що ДР (4.55) не можна розвязати відносно але для нього можлива параметризація 
Запишемо співвідношення 
Домножимо першу рівність на 
:
