Реферат: Диференціальні рівняння першого порядку, не розвязані відносно похідної

1. Основні поняття і означення, теорема про достатні умови існування і єдності розв’язку.

Диференціальне рівняння першого порядку, не розв’язані відносно похідної має вигляд

(5.1)

Найбільш часто зусрічаються диференціальні рівняння першого порядку -ої степені.

Означення 5.1. Функція , визначена і

(5.2)

неперервнодиференційовна на називається розв’язком Д.Р. (5.1), якщо вона після підстановки перетворює Д.Р. (5.1) в

тотожність

Означення 5.2. Будемо говорити, що рівняння визначає розв’язок Д.Р.(5.1) в нормальній формі, якщо воно визначає як функцію і вона являється розв’язком Д.Р.(5.1).

Означення 5.3. Рівняння , ,, визначає розв’язок Д.Р.(5.1) в параметричній формі, якщо

Криві на ел., які відповідають розв’язкам, будемо називати

Задача Коші - задача знаходження розв’язків, які задовільняють умови .

Означення 5.4. Говорять, що задача Коші для Д.Р.(5.1) з початковими умовами має єдиний розв’язок, якшо через в достатньо малому околі її проходить стільки , скільки напрямків поля визначає Д.Р. в цій точці. В противному – не єдиний розв’язок.

Теорема 5.1. (про існування і єдиність розв’язку задачі Коші).

Якщо функція задовільняє наступним умовам:

а) Являється визначеною і неперервною разом зі своїми ЧП в деякому замкненому околі т.;

б);

в);

то Д.Р.(1) має єдиний розв’язок , визначений і неперервно диференційовний в околі т , задовільняючий умови і такий, що

► Без доведення ◄

Припустимо, що розв’язуючи Д.Р.(1) відносно , ми знайдемо дійсні розв’язки

(5.3)

де визначені в обл. так, що маємо Д.Р. першого порядку, розв’язаних відносно . Припустимо, що в точці , напрямок поля, визначений кожним Д.Р. (5.3), різний. Так що різних рівнянь не можуть дотикатися друг друга на .

Нехай кожне Д.Р. (5.3) на має загальний інтеграл

(5.4)

Означення 5.5. Сукупність інтегралів (5.4) будемо називати загальним інтегралом Д.Р. (5.1) в обл. .

Інколи замвсть співвідношення (5.4) записують

(5.5)

Якщо поле на не задовільняє сказаному вище, тобто існує хоча б одна точка , в якій значення хоча б двох функцій співпали, то відповідаючі Д.Р. дотикаються друг друга в точці . Тому крім Д.Р. (5.3), будуть ще склеєні . Всі вони будуть входити в (5.4) або (5.5).

В загальному випадку Д.Р. (5.1) не удається розв’язати відносно в елементарних функціях. В цих випадках шукають однопараметричне сімейство в вигляді

(5.6)

яке називається загальним інтегралом Д.Р. (5.1).

Якщо сімейство задано в вигляді

(5.7)

то воно називається загальним розв’язком Д.Р. (5.1)

Зауважимо, що в (5.6) можуть входити і розв’язки Д.Р. виду (5.3), коли -комплексні. Ми таких Д.Р. не будемо розглядати, тому відповідні їм розв’язки треба виключати.

Сімейство , заданих в параметричному вигляді

(5.8)

будемо називати загальними розв’язками Д.Р. в параметричній формі.

Означення 5.6. Розв’язок Д.Р. (5.1) будемо називати частинним розв’язком, якщо в кожній його точці задача Коші має єдиний розв’язок.

Означення 5.7. Розв’язок називається особливим розв’язком, якщо в кожній його точці порушується єдинність розв’язку задачі Коші.

Аналогічно Д.Р., розв’язаним відносно , Д.Р. (5.1) може мати розв’язки, які являються ні частинними, ні особливими.

Аналіз частинних і особливих розв’язків для цих рівнянь більш складний. Зауважимо, що в випадку (5.3) розв’язок буде особливим, якщо буде особливим хоча б для одного з Д.Р. (5.3).

Приклад 5.1.

(5.9)

З (5.9) маємо:

Тоді - загальний інтеграл.

або . Цей загальний інтеграл є накладенням сімейств двох (мал. 5.1).

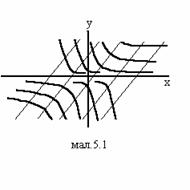
Розв’язок задачі Коші для Д.Р. (5.9) в кожній точці площіни являється єдиним. В точці ми маємо два напрямки поля:; І через цю точку проходить два

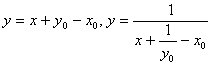, якщо (5.11)

і , якщо .

Розв’язки (10),(11) – частинні розв’язки. Особливих розв’язків немає.

2. Знаходження кривих, підозрілих на особливий розв’язок.

Припустимо, що Д.Р. (5.1) представлено в формі (5.3). При досліджені на особливий розв’язок рівнянь виду (5.3) ми прийшли до висновку, що ці розв’язки можливі на тих кривих, на яких являється необмеженою. Але в переході від Д.Р. (5.1) до рівнянь (5.3) є недоцільність при визначені особливих розв’язків, так як .