Реферат: Теорія виробництва

Сукупний продукт змінного фактора зростає у мі­ру того, як збільшуються затрати праці. Однак це зростання затухаюче. Більше того, настає момент, ко­ли збільшення кількості праці не збільшує, а змен­шує загальні результати виробництва. Це означає, що виробничий процес перенасичений працею, яка не може ефективно використовуватися за даного обсягу капіталу. У нашому прикладі це відбувається при співвідношенні К/L = 1/2.

Зазначені залежності можна показати графічно. На рис.5 показано криву сукупного продукту. Во­на відображає, як змінюється випуск продукції при зміні одного з факторів виробництва, тоді як інші за­лишаються незмінними.

Середній продукт змінного фактора можна визна­чити, якщо виміряти нахил променя, проведеного від початку координат через відповідну точку кривої су­купного продукту. Так, нахил променя ОА можна ви­значити через співвідношення координат точки А: Q1/L1. Це буде середній продукт у цій точці.

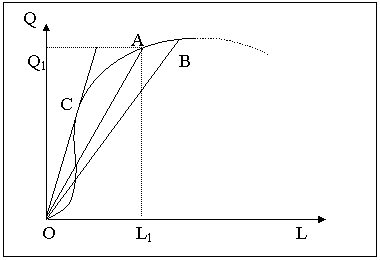Рис.5. Крива сукупного продукту змінного фактора

Середній продукт досягне свого максимуму за умови використання кількості праці, яка відповідає точці дотику променя, що виходить від початку коор­динат, та кривої сукупного продукту. На рис.5 це точка С.

Якщо проведемо дотичні до кожної точки на кри­вій сукупного продукту та знайдемо тангенси кутів, що вони утворюють з віссю X, то отримаємо гранич­ний продукт. Криві середнього та граничного продук­тів подано на рис.6.

Середній продукт буде збільшуватися доти, поки граничний продукт буде більший за нього. Якщо до виробництва залучається нова порція ресурсу, продук­тивність якої більша за середню, то таке залучення, звичайно, збільшить і середній показник. Навпаки, якщо гранична продуктивність змінного фактора ви­явиться менше середньої, то нове залучення змен­шить середні показники. Тому свого максимального значення середній продукт змінного фактора досяга­тиме в точці перетину кривих середнього та гранич­ного продуктів, тобто при АР = МР. У нашому при­кладі ця точка лежить в інтервалі затрат праці від 50 до 60 люд.-год.

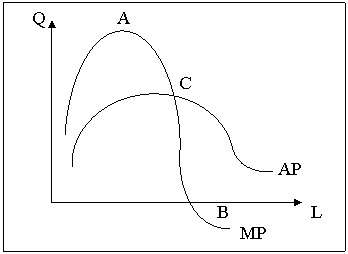Рис.6. Криві середнього та граничного продуктів

Слід звернути увагу на одну досить важливу залежність спрямованості динаміки граничного продукту від збільшення змінного фактора. Граничний продукт досягає свого максимуму в точці А, а потім починає зменшуватися. Більше того, після досягнення нуля у точці В граничний продукт набуває від'ємного значення. З цього моменту сукупний продукт починає зменшуватися при збільшенні змінного фактора. Ця залежність є досить стійкою, що дає змогу вважати ї економічним законом. Закон спадної граничної продуктивності полягає в тому, що, починаючи з певного обсягу збільшення використання одного з факторів виробництва, в той час як інші фактори залишаються незмінними, супроводжується зменшенням граничного продукту цього фактора. Це означає, ще збільшення обсягу випуску продукції обмежене, якщо змінюється тільки один фактор. Точка зменшення граничної продуктивності — це межа використання змінного фактора, за якою його граничний продукт починає зменшуватися.

Дія закону спадної граничної продуктивності стає очевидною, якщо взяти за приклад вирощування кар­топлі на присадибній ділянці чи дачі. Якщо вдвічі збільшити кількість годин роботи на ній проти нор­мального рівня, то кількість зібраної картоплі зросте у меншій пропорції. Якби такої залежності не існува­ло, то все сільське господарство світу можна було б помістити на одному гектарі землі, сконцентрувавши там усі витрати праці.

З'ясування динаміки обсягів виробництва залежно від динаміки змінного фактора для конкретного вироб­ництва має важливе практичне значення. Вона вико­ристовується насамперед для визначення меж, в яких доцільно вести виробництво з точки зору раціоналіза­ції використання факторів. Для короткотермінового пе­ріоду можна виділити три стадії виробництва:

перша стадія: від початку виробництва до до­сягнення середнім продуктом максимального значен­ня. Вона характеризується надлишком капіталу та недостачею праці, що призводить до перевитрат ре­сурсів та, як правило, до збитків підприємця;

друга стадія: від максимального значення се­реднього продукту до досягнення нульового значення граничного продукту. Ця стадія найпривабливіша для виробника, оскільки досягається нормальна збалансо­ваність факторів виробництва;

третя стадія: після досягнення граничним продуктом нульового значення. На ній виробництво стає перенасиченим працею і найчастіше призводить до збитків виробника.

Іншою сферою використання досліджуваних зако­номірностей може бути прийняття рішень з оптимізації структури затрат на виробництво. Припустимо, що існує дві дільниці, які виробляють однакову продук­цію. Як маневруючи перерозподілом фіксованої кіль­кості праці між ними в короткотерміновому періоді досягти більших обсягів виробництва?

Щоб відповісти на це запитання, слід порівняти граничні продукти змінного фактора на цих двох діль­ницях. Якщо при певному розподілі праці між діль­ницями МР1>МР2, то ресурси треба перерозподілити на користь першої дільниці, якщо співвідношення протилежне (МР1 < МР2) — на користь другої. Мак­симальний обсяг продукції з двох дільниць підприє­мець отримає тоді, коли граничні продукти на двох дільницях зрівняються: МР1 = МР2. Уміння оцінити граничні продукти змінного фактора та максимізувати результати від його використання є однією з скла­дових мистецтва управління.

3. Аналіз ізоквант можна використовувати для ви­значення можливостей заміщення одного фактора ви­робництва іншим у процесі їх використання. Гранич­на норма технологічного заміщення працею капіталу (МRTSLK) визначається розміром капіталу, який може замінити кожна одиниця праці, не викликаючи при цьому зміни обсягів виробництва:

МRTSLK = -DK/DL. (2)

Форма ізокванти (випукла до початку системи ко­ординат) показує, що гранична норма технологічного заміщення зменшується при просуванні вниз уздовж ізокванти. Це означає, що кожна година людської праці здатна замінити все меншу кількість капіталу. Причина зменшення граничної норми технологічного заміщення полягає в тому, що фактори виробництва мають властивість доповнювати один одного. Кожен з них не може робити те, що може робити інший, або якщо й може, то гірше.

Граничну норму технологічного заміщення факто­рів виробництва можна розрахувати не тільки через зіставлення їх приростів, а й через граничні продук­ти. Дійсно, якщо при зменшенні капіталу з К1 до К2 та зростанні кількості праці з L1 до L2 (див. рис.2) виробник залишається на тій самій ізокванті, то справедливою буде така рівність:

DL MPL= -DK MPK (3)

Тоді

МRTSLK = -DK/DL= MPL/ MPK. (4)

Оскільки залежність (4) характеризує нахил ізо­кванти в кожній точці кривої, то в подальшому вона буде використана для обгрунтування точки рівноваги виробника.

Хоча спадна гранична норма технологічного замі­щення працею капіталу властива для абсолютної біль­шості виробничих процесів, існує цілий ряд винятків, де ця залежність дещо інша. Розглянемо кілька з них.

1. Фактори виробництва можуть використову­ватися лише у певній пропорції. Прикладом є спів­відношення комп'ютерів та операторів ПЕОМ. Якщо кількість годин роботи комп'ютера протягом робочого дня фіксована, то збільшення кількості операторів не призведе до зростання обсягів продукції. Справедли­вим буде також зворотне твердження: при фіксованій кількості операторів неможливо досягти зростання обсягів виробництва за рахунок збільшення кількості комп'ютерів. У цьому випадку ізокванта матиме ви­гляд прямого кута, а гранична норма технологічного заміщення дорівнюватиме нулю (рис.7).

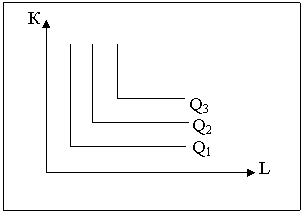Рис.7. Ізокванти при фіксованій пропорції факторів виробництва

2. Повне заміщення факторів виробництва. За такої умови ізокванта мала б вигляд прямої лінії з постійним нахилом, який дорівнює 1. Однак цю ситуа­цію слід розглядати лише як теоретичну абстракцію: в реальному житті повне заміщення факторів вироб­ництва в принципі не можливе.

4. На відміну від короткотермінового періоду в довго­терміновому періоді всі фактори виробництва змінні. Якщо зберегти припущення, що для виробництва вико­ристовується тільки два фактори (праця та капітал) і технологія залишається незмінною, то зростання вироб­ництва в довготерміновому періоді можна розглядати як таке, що відбувається при незмінному співвідношенні факторів виробництва. Це означатиме, що вироб­ництво збільшуватиметься тоді, коли використання йо­го факторів зростатиме за променем, спрямованим від початку координат (рис.8). При цьому можливі кіль­ка варіантів реакції середнього продукту на збільшення масштабів виробництва: 1) зростаюча; 2) нейтральна; 3) спадна. Тут проявляються різні наслідки так званого ефекту масштабу виробництва.

Зростаюча реакція середнього продукту відбувається на позитивний ефект збільшення масштабів виробницт­ва. Він може досягатися за рахунок таких факторів:

Поділ праці. На більших підприємствах можлива глибша внутрішня спеціалізація, що дає ефект зростан­ня продуктивності праці і, отже, зменшення затрат.

Поліпшення управління. Поглиблена спеціалі­зація поширюється і на управлінську діяльність. По­ява управлінців, які спеціально займаються марке­тингом, рекламою, постачанням, організацією науко­во-технічних робіт тощо, допомагає збільшити ефек­тивність діяльності підприємства в цілому, що прояв­ляється в зростанні середнього продукту.

Збільшення масштабів виробництва найчастіше не вимагає пропорційного збільшення всіх ресурсів. Скажімо, витрати часу лектора не збільшаться, якщо в аудиторії на лекції буде не одна, а дві групи студентів.