Реферат: Комп’ютерна економетрія

При рішенні задачі на максимум загальної собівартості були отримані наступні результати:

; ; ; ;

Потрібно:

1. Сформулювати пряму оптимізаційну на максимум загальної собівартості, вказати оптимальну виробничу програму.

Нехай ; ; ; - обсяги виробництва продукції кожного виду.

Цільова функція:

Функціональні обмеження:

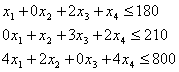
Прямі обмеження:

Оптимальна виробнича програма полягає у випуску 95 од. першої продукції, 210 од. другої продукції, 0 од. третьої продукції і 0 од. четвертої продукції.

Третій і четвертий вид продукції випускати не вигідно, тому що витрати перевищують ціну.

2. Сформулювати двоїсту задачу і знайти її оптимальний план.

Нехай ; ; - двоїсті оцінки типів ресурсів відповідно.

Цільова функція:

Функціональні обмеження:

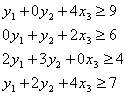
Прямі обмеження:

Знайдемо оптимальний план цієї задачі, використовуючи теорему подвійності:

Насамперед, перевіримо, чи є зазначений в умові задачі план припустимим рішенням:

По ресурсі I:

По ресурсі II:

По ресурсі III:

Отже, план оптимальний. Ресурс I залишається в надлишку, а ресурси II і III витрачаються цілком.

Скористаємося співвідношенням другої теореми подвійності:

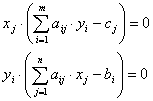
т.к. і ,те

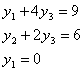
Обчислимо значення цільової функції двоїстої задачі:

,

таким чином приведений в умові план є оптимальним.

3. Проаналізувати використання ресурсів в оптимальному плані.

Ресурс I є недефіцитним ( ). Ресурси II і III є дефіцитними, причому ресурс III більш дефіцитний, чим ресурс II ( ).

Знайдемо норму заменяемости для дефіцитних ресурсів:

Отже, ресурс III у 1,5 рази більш ефективний, чим ресурс II з погляду впливу на максимум продукції.

4. Визначити, як зміниться загальна вартість продукції і план випуску при збільшенні запасів сировини II і III виду на 120 і 160 од. відповідно й одночасному зменшенні запасів сировини I виду на 60 од.

Будемо вважати, що даної зміни обсягів ресурсів знаходяться в межах стійкості оптимального рішення (у межах стійкості двоїстих оцінок), тоді по третій теоремі подвійності маємо:

Запишемо вихідну і двоїсту ЗЛП зі зміненими обсягами ресурсів.

Вихідна:

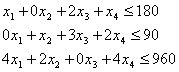
Двоїста:

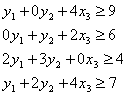
Скористаємося співвідношенням другої теореми подвійності:

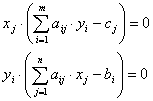
Розглянемо перші співвідношення (їхній два):

Отже, про нічого сказати не можна.

Отже, про нічого сказати не можна.

, (витрати більше ціни)

, (витрати більше ціни)

Розглянемо другі співвідношення:

, нічого сказати не можна

, друге обмеження звертається в рівність

, третє обмеження звертається в рівність

Запишемо систему рівнянь і вирішимо її:

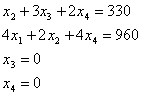
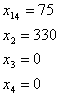
Це збігається з висновком, зробленим раніше на підставі теореми про оцінки.

5. Визначити доцільність включення в план виробу «Д» ціною 12 од. на виготовлення, якого витрачається по двох одиниці кожного виду сировини.

Це завдання виконується на основі третьої властивості двоїстих оцінок, тобто оцінки як визначення ефективності.

Розрахуємо показник ефективності для цієї продукції:

Отже, дану продукцію випускати доцільно (витрати менше ціни).

4-7

Економетрична модель може являти собою як дуже складну систему так і просту формулу, що може бути легко підрахована на калькуляторі. У будь-якому випадку вона вимагає знань по економіці і статистиці. Спочатку для визначення відповідних взаємозв'язків застосовуються знання по економіці, а потім для оцінки кількісної природи взаємозв'язків отримані за минулий період дані обробляються за допомогою статистичних методів.

Економічна діяльність часто буває сполучена з необхідністю прогнозування конкретної чи ситуації результатів конкретної діяльності. Математичні методи являють собою тот інструментарій, що дозволяє оцінити стан економічної системи і її елементів у майбутній момент часу. Дані методи звуться «стохастических» і знаходять широке застосування при дослідженні економічних відносин.

Економічні відносини, що складаються між різними економічними суб'єктами, можуть бути представлені у виді визначеної моделі, що описується сукупністю вимірних параметрів. У зв'язку з цим при вивченні економічної науки необхідно розглянути економетричні методи дослідження економічних відносин, що дозволяють моделювати економічну систему і кількісно неї описувати.

Економетричні моделі, як правило, використовуються в розробках прогнозів генетичного (дослідницького) характеру шляхом екстраполяції тенденцій розглянутих процесів і рішень. При цьому розрізняють формальну і прогнозну екстраполяцію. Формальна екстраполяція припускає повну незмінність тенденцій, що існували в минулому, прогнозна — допускає сполучення наявних тенденцій з деякими гіпотезами у відношенні закономірностей розвитку процесів, що випливають з їхньої логічної чи фізичної сутності. У своїй основі це сполучення уможливлює коректування результатів формальної екстраполяції або параметрів уже побудованої економетричної моделі виходячи з додаткових зведень, припущень. У доцільності такого коректування американський економіст П.Самуельсон помітив«...я підозрюю, що кращі прогнози, що не використовують формальних методів, так само гарні чи погані, як і кращі економетричні прогнози. Справді, на такі думки повинна наводити той факт, що майже всі економетрики, за рідкісним винятком, коректують параметри моделей за допомогою неформальних методів, вважаючи, що це поліпшує результати».