Реферат: Тригонометричні функції

1. Стисненням заготовки на прокатному стані на­зивають величину де і — товщини заготовки до і після прокатування. Доведіть, що -, де d — діаметр вала і — кут захвату.

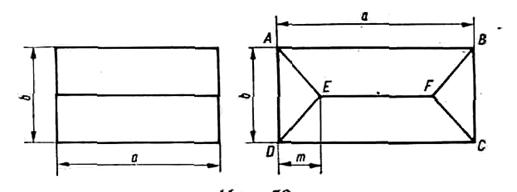
Вказівка. З прямокутного трикутника АОВ: ОВ = 0,5d cos, = 2.

2. Схили двосхилого і схили ABFE і CDEF чотири­схилого даху з горизонтальною площиною утворюють кут , а схили ADE і BCF — кут . Для якого даху — дво- чи чотирисхилого потрібно менше мате­ріалу?

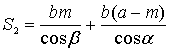Вказівка. Площа двосхилого даху , а чотирисхилого - . Щоб порівняти ці площі, розглянемо їх різницю

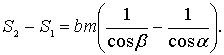
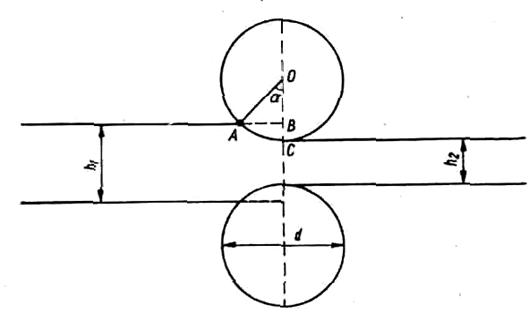
Оскільки b>0, m>0, 0<<90° і 0<<90°, то при < дістанемо S2 — S1 < 0; при = , S2-S1 = 0, а при > , S2 – S1 >0.

Отже, якщо всі схили обох дахів будуть однаково нахилені до горизонтальної площини, то на обидва дахи потрібна буде однакова кількість покрівельного матеріалу. Якщо схили ADE і BCF чотирисхилого даху матимуть більший кут нахилу, ніж схили АВEF і DCFE, то покрівельного матеріалу потрібно буде біль­ше, ніж для двосхилого, а при меншому куті — менше.

Границя функції

1. Температура нагрівання металевого стержня на відстані від місця нагрівання (до температури 1000 °) визначається формулою f(x) = де х – відстань у дециметрах. Визначте граничні значення температури стержня на відстані 1 м від місця нагрівання. Чи можна такий стержень взяти в руку?

Відповідь.

2. Яку роботу треба виконати, щоб викачати воду з ями глибиною і площею дна ?

Розв'язання. Поділимо глибину ями на п рівних частин і в думці проведемо горизонтальні площи­ни, які ділять об'єм ями на п рівних частин. Висота кожного шару дорівнюватиме м, а маса 1000 кг = 9800 Н.

Вважатимемо, що кожний з шарів води піднімають на висоту, яка дорівнює відстані від нижньої площини до поверхні води. Тоді висоти піднімання послідовних частин води дорівнюватимуть: , , ,...,, а набли­жені значення роботи піднімання цих частин визнача­тимуться так:

.

Отже, наближене значення роботи піднімання всієї води становитиме:

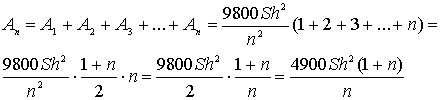
Вся робота, очевидно, дорівнює:

Поняття похідної функції

1. (t) — 3t2 — 4t — рівняння прямолінійного ру­ху матеріальної точки (s, м; t, с). Знайдіть середню швидкість цієї точки за проміжок часу від t1 = 2 с до t2 = 5 с.

Розв'язання. Середня швидкість матеріаль­ної точки за проміжок часу l є відношення відстані , пройденої точкою за цей проміжок часу, до величини проміжку часу

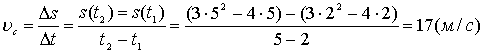
2. Знайдіть швидкість руху тіла в момент часу і = 2 с, якщо закон руху задано формулою .

Відповідь. = 16 м/с.

3. Під час нагрівання тіла його температура Т змі­нюється залежно від часу нагрівання t за законом Т(t) = 0,4 t2. З якою швидкістю змінюється температура тіла в момент t = 10 с?

4. Об'єм газу V при температурі t0 визначається формулою V = 1 + 0,0075 t. Визначте швидкість змі­ни об'єму газу при будь-якій температурі.

5. Сила струму в амперах змінюється залежно від часу за законом J = 0,2 t2, де t — час у секундах. Знайдіть швидкість зміни сили струму наприкінці десятої секунди.