Реферат: Теорія імовірностей та математична статистика
Теоретичні відомості:
Набір експерементальних даних будем позначати![]() x
x![]() , …,x
, …,x![]() . Однорідний набір спостережень називається вибіркою з генеральної сукупності. Генеральна сукупність - універсальна множина значень(проявів) цього явища. Кількість елементів вибірки називають об'ємом вибірки. Вибіркові значення називають ще й статистичним розподілом, якщо їх спеціальним чином перетворити. З однієї генеральної сукупності можна отримати різні вибірки, тому вибірку називають статистичною змінною, які в свою чергу бувають: дискретними або наперервними.
. Однорідний набір спостережень називається вибіркою з генеральної сукупності. Генеральна сукупність - універсальна множина значень(проявів) цього явища. Кількість елементів вибірки називають об'ємом вибірки. Вибіркові значення називають ще й статистичним розподілом, якщо їх спеціальним чином перетворити. З однієї генеральної сукупності можна отримати різні вибірки, тому вибірку називають статистичною змінною, які в свою чергу бувають: дискретними або наперервними.
Весь аналітичний процес можна поділити на побудову варіаційного ряду та табличне, графічне, аналітичне представлення цієї вибірки.
Варіаційним рядом вибірки x![]() , …,x
, …,x![]() (1) називається сукупність всіх елементів вибірки розміщених у порядку неспадання величин їх значень.
(1) називається сукупність всіх елементів вибірки розміщених у порядку неспадання величин їх значень.
Нехай x![]() , … , x
, … , x![]() (2) - варіаційний ряд вибірки (1), тоді можна побудувати частотну таблицю (3):
(2) - варіаційний ряд вибірки (1), тоді можна побудувати частотну таблицю (3):
| X | y | … | y |
| V | n | … | n |
де y![]() - найменше значення варіаційного ряду (2),
- найменше значення варіаційного ряду (2),
n![]() - кількість його повторень, і т.д.
- кількість його повторень, і т.д.
Якщо випадкові змінні неперервні, то діапазон зміни
вибіркових значень x![]() - x
- x![]() розбивається на r груп
розбивається на r груп ![]() ,
,
де
z![]() - середина першого інтервала.
- середина першого інтервала.
z![]() - середина r-того інтервала.
- середина r-того інтервала.
r вибирається з умови: 2![]()
![]()
Нехай n![]() попадає на z
попадає на z![]() , … , n
, … , n![]() попадає на z
попадає на z![]() .
.
Тоді частотна таблиця набуде вигляду:
| Z | z | … | z |
| V | n | … | n |
Де n![]() + … + n
+ … + n![]() =n
=n
Найчастіше для графічного зображення вибірки використовують:
Графік (діаграма частот).
Полігон частот.
Гістрограма.
Нехай маєм частотну таблицю (3). Діаграмою частот називається сукупність вертикальних відрізків поставлених в точках y![]() , … , y
, … , y![]() , з довжиною n
, з довжиною n![]() , … , n
, … , n![]() .
.
Полігон частот, це ламана лінія, що зєднує точки з кординатами (x![]() ,n
,n![]() ).
).
Гістрограма - сукупність прямокутників, центри основ яких лежать в точках z![]() (якщо маєм вибірку з неперервної генеральної сукупності) і x
(якщо маєм вибірку з неперервної генеральної сукупності) і x![]() (якщо маєм вибірку з дескретної генеральної сукупності).
(якщо маєм вибірку з дескретної генеральної сукупності).
Аналітично статистичні дані представляються як правило емпіричною функцією розподілу або певними статистиками. Нехай маєм частотну таблицю (3), то емпіричною функцією називається:
F![]() =
=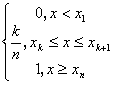 (6)
(6)
де к - кількість елементів вибірки, що неперевищують x.
Числові характеристики статистичного матеріалу поділяються на:
Статистики локації(центральної тенденції).
Розсіювання.
Числові характеристики форми.
Числові характеристики центральної тенденції.
Медіана - той елемент вибірки(якщо елементів непарна кількість) який поділяє вибірку по об'єму на дві рівні частини.Якщо елементів є парна кількість то медіана є проміжком.
Мода - той елемент частотної таблиці, який має найбільшу частоту, тобто найчастіше зустрічається у вибірці.
Середнє, якщо випадкові змінні дискретні і (3) - її частотна таблиця обчислюється за формулою: ![]() =
=![]() або
або ![]() =
=![]() .
.
Числові характеристики розсіювання.
Варіанса: S![]() .
.
Середньоквадратичне відхилення: S=![]() .
.
Варіація(мінливість): V=![]() .
.
Розмахом: ![]() =x
=x![]() -x
-x![]() .
.
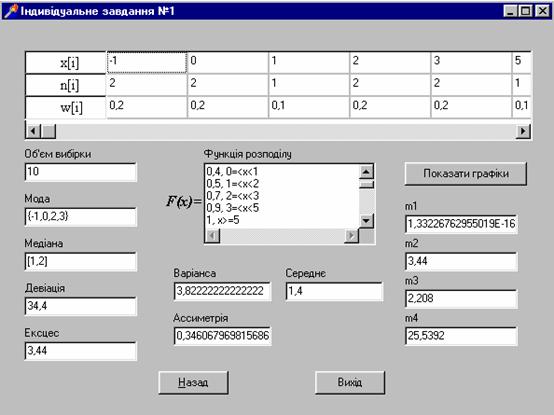
Приклад роботи програми:
 |