Реферат: Теореми про диференціальні функції

Рис.2

Оскільки функція f(х)= sin x і її многочлени Тейлора є функції непарні, то на рис. 2 зображена лише „половина” графіків.

знайти формулу Маклорена для функції f(х)=ln (1 + х).

Знаходимо значення даної функції і її похідних при х = 0:

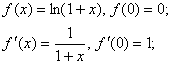
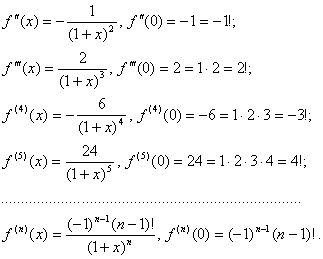
Підставляючи значення похідних у формулу Маклорена, маємо

.

Розкласти за формулою Маклорена функції:

а) б) в) , a Î R.

Аналогічно до попереднього розв’язання маємо:

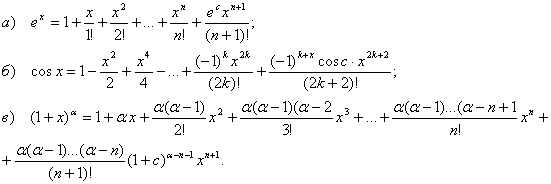
Знайти многочлен Тейлора для функції , який зображав би цю функцію на відрізку [-1; 1] з точністю до 0,001. Обчислити наближене значення е.

З попереднього прикладу маємо

підберемо таке п, при якому модуль залишкового члена був би меншим від числа 0,001, маючи на увазі, що | х | £ 1, число с лежить між 0 і х та ес < е|х| < е:

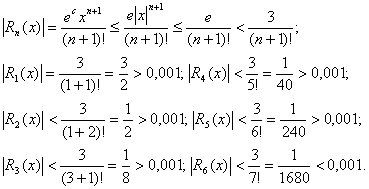
Отже, п = 6, тому з точністю до 0,001 справедлива наближена формула

.

Якщо в цій формулі покласти, наприклад, х = 1, то матимемо наближене значення числа е:

.

Знайти многочлен Тейлора Р3 (х – 1) третього степеня відносно двочлена х – 1 для функції .

Маємо

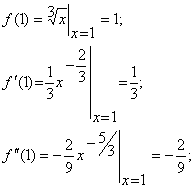
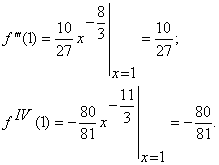
Поклавши у формулі Тейлора (1) х0 = 1 і п = 3, дістанемо

,

де с лежить між 1 і х, тому

.

Формулу (1) можна записати у вигляді

. (10)

Коли функція f(х) є многочленом Рп (х) степеня п, то похідна , тому формула (10) матиме вигляд

. (11)

Ця формула називається формулою Тейлора для многочлена.

Приклади

Розкласти многочлен Р3(х) = 1 – 2х + 3х2 – 4х3 за степенями бінома х + 1.

Скориставшись формулою (11) при х0 = –1, маємо

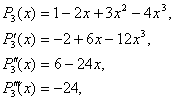
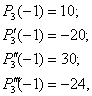
тому

.

Розкласти многочлен Рп(х) = (b + x)n за степенями х.

Маємо Рп(0) = bn, , тому, поклавши у формулі (11) Рп(х) = (b + x)n , х0 = 0, дістанемо відому формулу бінома Ньютона:

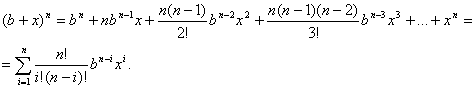(12)