Реферат: Розв'язування систем лінійних рівнянь методом Гаусса
Одним з найпоширеніших методів розв'язування систем лінійних рівнянь є метод послідовного виключення невідомих, або метод Гаусса. Цей метод запропонований К. Гауссом і ґрунтується на елементарних перетвореннях системи рівнянь (п. 2.1).
Нехай маємо систему (9), яка містить т рівнянь і п невідомих. Очевидно, серед коефіцієнтів аі1 хоча б один відмінний від нуля. Якщо ж а11 = 0, то першим в системі (9) запишемо те рівняння, в якому коефіцієнт при х1 відмінний від нуля. Позначимо цей коефіцієнт через а11.
Перетворимо систему (9), виключаючи x1 в усіх рівняннях, крім першого. Для цього помножимо перше рівняння на — ![]() і додамо до другого, потім помножимо перше рівняння на —
і додамо до другого, потім помножимо перше рівняння на — ![]() і додамо до третього і т. д. При цьому може статись так, що друге невідоме х2 також не входить в усі рівняння з номером і > 1. Нехай xk — невідоме з найменшим номером, яке входить в будь-яке рівняння, не рахуючи першого. Дістанемо систему
і додамо до третього і т. д. При цьому може статись так, що друге невідоме х2 також не входить в усі рівняння з номером і > 1. Нехай xk — невідоме з найменшим номером, яке входить в будь-яке рівняння, не рахуючи першого. Дістанемо систему
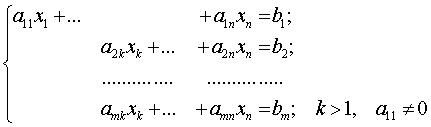
Застосовуючи до всіх рівнянь, крім першого, таку саму процедуру і виконавши ряд елементарних перетворень, дістанемо систему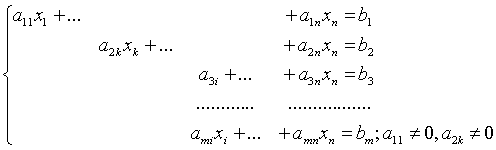
Якщо продовжити цей процес, то матимемо систему
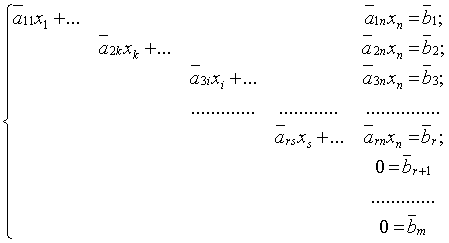
Таку систему рівнянь називають східчастою або трапецієподібною. Дослідимо цю систему.
1. Якщо система містить рівняння виду 0 = bt і bt ≠ 0, то вона очевидно несумісна.
2. Нехай система (22) не містить рівнянь виду 0 = bt (bt ≠ 0). Назвемо невідомі х1, xk, хl, ..., xs, з яких починаються перше, друге, ..., r-е рівняння, основними, а всі інші, якщо вони е, вільними. Основних невідомих за означенням r. Надаючи вільним невідомим довільні значення і підставляючи ці значення в рівняння системи, з r-го рівняння знайдемо хs. Підставляючи це значення в перші r — 1 рівнянь і, піднімаючись вгору по системі, знайдемо всі основні невідомі. Оскільки вільні невідомі можуть набувати будь-яких значень, система має безліч розв'язків.
3. Нехай в системі (22) г — п. Тоді вільних невідомих немає, тобто всі невідомі основні і система (22) має так званий трикутний вигляд:
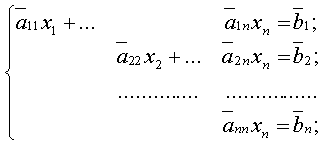
З останнього рівняння системи знайдемо хп, і, піднімаючись по системі вгору, знайдемо всі інші, невідомі. Отже, в цьому випадку система має єдиний розв'язок.
Зауваження 1. Викладений нами метод послідовного виключення змінних називають ще алгоритмом Гаусса. Він складається з однотипових операцій і легко реалізується на сучасних ЕОМ.
Зауваження 2. При розв'язуванні системи лінійних рівнянь методом Гаусса зручніше приводити до трикутного чи трапецієподібного вигляду не саму систему рівнянь, а розширену матрицю цієї системи, тобто матрицю, утворену приєднанням до матриці її коефіцієнтів стовпця вільних членів. Виконуючи над рядками розширеної матриці елементарні перетворення, приходимо до розв'язку системи.
Приклад
Розв’язати систему рівнянь методом Гаусса:
а) 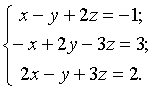 б)
б) 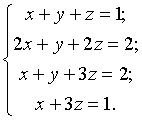 в)
в) 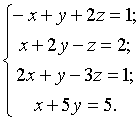
![]() а) Виконуємо елементарні перетворення над рядками розширеної матриці даної системи (позначатимемо це символом )
а) Виконуємо елементарні перетворення над рядками розширеної матриці даної системи (позначатимемо це символом )
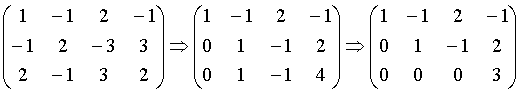
Таким чином, система а) еквівалентна системі
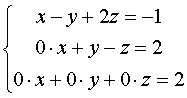
в останньому рівнянні вільний член дорівнює двом, а коефіцієнт при невідомих дорівнюють нулю (тобто 0 = 2), тому система несумісна.
б) Маємо
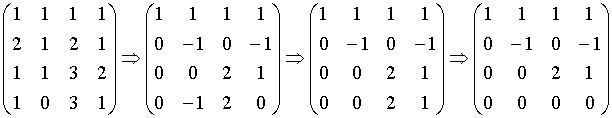
Отже система б) еквівалентна системі трикутного вигляду
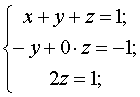 і має єдиний розв’язок :
і має єдиний розв’язок : ![]()
в) Маємо

Отже система в) еквівалентна системі трапецієподібного вигляду
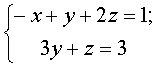
і має безліч розв’язків. З останньої системи знаходимо
![]()
Таким чином розв’язки системи в) мають такий вигляд ![]()
Зазначимо, що жодну з наведених у цьому прикладі систем не можна розв’язувати ні за формулами Крамера, ні матричним способом.
Література:
Дубовик В.П., Юрик І.І., Вища математика: навч. посібник – К.: А.С.К. 2001 – 648с., іл. – (Унів. б-ка) – бібліорг. с. 632-633