Реферат: Розклад вектора на складові на площині і в просторі. Декартові система координат

Мета. Ознайомитись з поняттям про базис на площині і в просторі; та координати вектора.

Розклад вектора з двома не колінеарними векторами на площині.

Система координат на площині.

Розклад вектора за трьома не колінеарними векторами в просторі.

Система координат в просторі.

Теорема.

Будь – який на площині можна подати, про чому єдиним чином, у вигляді лінійної комбінації двох не колінеарних векторів.

, де

- не колінеарні вектори

- числа.

Доведемо це. Нехай маємо на площині три вектори , причому не колінеарні.

Покажемо, що

Відкладемо їх від спільної точки і на як на діагоналі будуємо паралелограм

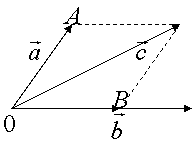
колінеарні

тому

Найчастіше базисні вектори вибирають одиничними і взаємно перпендикулярними, позначають їх .

Тоді , де x, y – координати вектора в базисі . Якщо відкласти ці вектори в певному порядку від однієї точки і через них провести прямі (осі координат), то одержимо прямокутну систему координат на площині.

Щоб побудувати в системі координат, треба відкласти точку з цими координатами і ця точка буде кінцем вектора, а початком – початок координат

Теорема.

Будь – який вектор в просторі можна подати, при чому єдиним чином, у вигляді лінійної комбінації трьох некомпленарних векторів

, де

- не колінеарні вектори

- числа

(див задачу з попереднього уроку)

Найчастіше їх вибирають одиничними і взаємно перпендикулярними, позначають .

Тоді , де

- координати в базисі .

, х – абсцис, у – ордината, z – апліката

якщо відкласти ці вектори в певному порядку від однієї точки і через них провести прямі (осі координат), то одержимо прямокутну систему координат в простора.