Реферат: Поняття про ряд Тейлора
Степеневий ряд ![]() називається рядом Тейлора.
називається рядом Тейлора.
Для розкладу в ряд Тейлора діалоговому режимі діємо за схемою:
Series → x=1 → Power Series
Power Series
![]()
Порівняння графіків функції y=lnx і многочлена ![]()
plot 2D + Rectangular
![]()
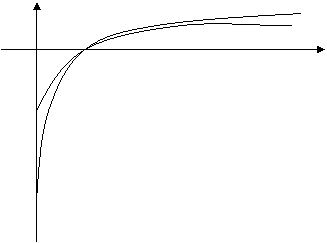
1
0 1 1,5 2
-2
-4
-5
Ряд Тейлора
Досі ми вивчали властивості суми заданого степеневого ряду. Вважатимемо тепер, що функція задана, і з’ясуємо, за яких умов цю функцію можна подати у вигляді степеневого ряду і як знайти цей ряд.
Нехай функція f(x) є сумою степеневого ряду
![]() (1)
(1)
в інтервалі (х0-R;x0+R). У цьому разі кажуть, що функція f(x) розкладена в степеневий ряд в околі точки х0 або за степенями х-х0. Знайдемо коефіцієнт ряду (1). Для цього, згідно з властивістю 40 послідовно диференціюємо ряд (1) і підставлятимемо в знайдені похідні значення х=х0:
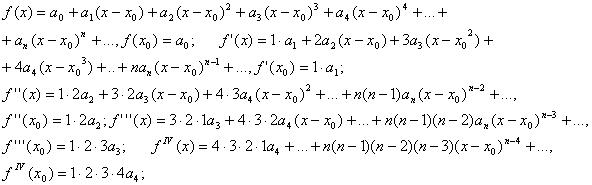
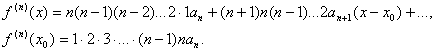
Звідси знаходимо коефіцієнти
![]()
Підставивши значення цих коефіцієнтів у рівність (1) дістанемо
![]()
ряд
![]() (2)
(2)
називається рядом Тейлора функції f(x). Отже, доведено таку теорему.
Теорема 1. Якщо функцію f(x) в інтервалі (х0-R;x0+R) можна розкласти в степеневий ряд, то цей ряд єдиний і є рядом Тейлора даної функції.
Нехай тепер f(x) – довільна нескінчене число разів диференційована функція. Складемо для неї ряд (2). Виявляється, що сума ряду (2) не завжди збігається з функцією f(x). Інакше кажучи, ряд (2) формально складено. Встановимо умови, за яких сума ряду (2) збігається з функцією f(x).
Теорема 2. Для того щоб ряд Тейлора (2) збігався до функції f(x) в інтервалі (х0-R;x0+R), тобто
![]()
необхідно і додатно, щоб в цьому інтервалі функція мала похідні всіх порядків і залишковий член її формули Тейлора прямувала до нуля при ![]() для всіх х з цього інтервалу:
для всіх х з цього інтервалу:
![]() (3)
(3)
Відомо, що для функції, яка має похідні всіх порядків, справедлива формула Тейлора
![]() (4)
(4)
де
![]() (5)
(5)
- залишковий член формули Тейлора у формулі Лонгранжа.
Якщо позначити n –у частину суму ряду (2) через Sn(x), то формула (4) матиме вигляд
![]() (6)
(6)
Нехай f(x) - сума ряду, тобто
![]()
тоді з формули (6) випливає умова (3). Навпаки, якщо виконується умова (3), то з формули (6) випливає рівність ![]() .
.
Таким чином, функцію f(x) можна розкласти в ряд Тейлора в інтервалі (х0-R;x0+R) тоді і тільки тоді, коли виконуються такі умови: 1). Вона має похідні всіх порядків; 2). Залишковий член формули Тейлора (5) прямує до нуля при n→0 і всіх ![]() (х0-R;x0+R).
(х0-R;x0+R).
Безпосередня перевірка цих умов нерідко виявляється непростою задачею. Доведемо теорему, яка дає досить прості достатні умови розкладання функції в ряд Тейлора.
Теорема 3. Якщо функція f(x) в інтервалі (х0-R;x0+R) має похідні всіх порядків та існує число М>0 таке, що
![]() (7)
(7)
де ![]() , то функцію f(x) можна розкласти в ряд Тейлора.
, то функцію f(x) можна розкласти в ряд Тейлора.
Відповідно до теореми 2 досить перевірити умову (3). В силу нерівностей (7) залишковий член формули Тейлора (3) задовольняє нерівність (7)
![]() (8)
(8)
Побудуємо степеневий ряд
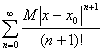 . (9)
. (9)
оскільки
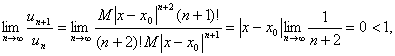
то за ознакою Д’Амламбера ряд (9) збіжний на всій числовій осі.
Для збіжного ряду
![]()
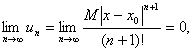
тоді з нерівностей (8) знаходимо
![]()
Вправи для самостійного розв’язання
Знайти суми таких рядів:
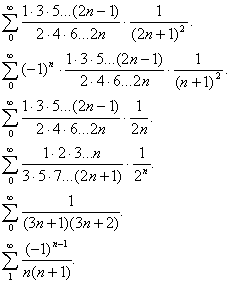
приклад (1)
Знайти три перших (відмінних від нуля) члени розкладу в ряд розв’язку рівняння
![]()
Шукаємо розв’язок у(х) у вигляді ряду Тейлора:
![]() ... .
... .
Маємо
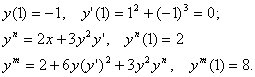
Отже,
![]()
Приклад 2.
Розглянемо розклад функції ![]() у ряд Маклорена
у ряд Маклорена
- Знаходимо функції і похіжні
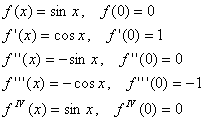
Знаходимо розклад функцій ![]() у ряд
у ряд
![]()
Залишковий член формули Пейнора
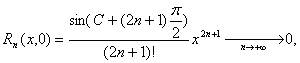
тому розклад буде справедливий при будь-якому значенні х.
Контрольні запитання
Що називають рядом Тейлора для функції f(x)?
Як знайти коефіцієнти ряду Тейлора?
Сформулювати і довести теорему про необхідні і достатні умови, за яких сума ряду Тейлора функції f(x) збігається з цією функцією.
Література
Дубовик “Вища математика”, Навчальний посібник. Київ 2001.
К.Г. Валєєв, І.А. Джаладова “Вища математика”. – Навчальний посібник, Київ 2002.