Реферат: Початки комбінаторики

1. При A={a, b, c} усіма комбінаціями по 2 з повтореннями є послідовності (a,a), (a,b), (a,c), (b,b), (b,c), (c,c). Їм відповідають усі можливі склади (2,0,0), (1,1,0), (1,0,1), (0,2,0), (0,1,1), (0,0,2).

2. Нехай m однакових кульок розкладаються по n різних ящиках так, що у першому ящику k1 кульок, у другому – k2 кульок, …, у n-му – kn кульок, причому m=k1+k2+…+kn. Пронумеруємо ящики від 1 до n. Задамо розподілення кульок як функцію, яка ставить у відповідність номеру ящика кількість кульок у ньому. Отже, маємо послідовність (k1, k2, …, kn), що є складом. Припишемо кожній кульці номер її ящика і утворимо послідовність номерів вигляду

(1, …, 1, 2, …, 2, …, n, …, n).

123 123 123

k1 k2 … kn

Як бачимо, множиною елементів, якими утворюється комбінація з повтореннями, тут є {1, 2, …, n}.

Комбінації по m елементів множини {a1, a2, …, an} з повтореннями складу (k1, k2, …, kn) можна взаємно однозначно поставити у відповідність послідовність довжини m+n-1 із m "1" і n-1 "0":

(1, …, 1, 0, 1, …, 1, 0, …, 1, …, 1).

123 123 123

k1 k2 … kn

Такій послідовності, у свою чергу, взаємно однозначно відповідає комбінація номерів місць у цій послідовності, на яких розташовані 1 (або 0). Кількість таких комбінацій є , що й є кількістю всіх можливих комбінацій по m елементів n-елементної множини з повтореннями.

6. Формули включень і виключень

Кількість елементів об'єднання двох множин, що не перетинаються, є сумою їх кількостей. Але якщо множини перетинаються, то елементи перетину при цьому додаванні кількостей враховуються двічі. Тому їх кількість треба один раз відняти:

|AÈB|=|A|+|B|-|AÇB|. (*)

При обчисленні |AÈBÈC| додавання |A|+|B|+|C| веде до того, що елементи кожного з перетинів |AÇB|+|BÇC|+|AÇC| враховуються двічі, тому їх треба по одному разу відняти. Якщо перетин AÇBÇC порожній, то в результаті кожний елемент об'єднання враховано по одному разу, і все гаразд. Якщо ні, то в результаті елементи цього перетину тричі додаються і тричі віднімаються, тобто у виразі

|A|+|B|+|C|–|AÇB|–|BÇC|–|AÇC|

не враховані. Отже, їх треба додати:

|AÈB|=|A|+|B|+|C|–|AÇB|–|BÇC|–|AÇC|+|AÇBÇC|. (**)

Вирази (*), (**) наводять на припущення, що в загальному випадку об'єднання n множин A1, A2, …, An

|A1ÈA2È…ÈAn|=|A1|+|A2|+…+|An|–|A1ÇA2|–|A1ÇA3|–…–|An-1ÇAn|+
+|A1ÇA2ÇA3|+…+|An-2ÇAn-1ÈAn|–…+(-1)n+1|A1ÇA2Ç…ÇAn|. (1)

Як бачимо, кількості елементів усіх можливих перетинів непарної кількості множин додаються, а парної – віднімаються. Формула (1) називається формулою включень і виключень.

Доведення формули (1) можна провести з використанням індукції за n, але тут ми його не наводимо.

Ця формула дає змогу за кількостями елементів у кожній з множин, в усіх можливих їх перетинах по дві, по три і т.д. множини обчислити кількість елементів об'єднання.

Приклад. Є група студентів, серед яких каву п'ють 12 (це множина A), чай – 10 (множина B), йогурт – 8 (C), каву і чай – 5 (AÇB), каву і йогурт – 4 (AÇC), чай і йогурт – 3 (BÇC), усі три напої – 1 (AÇBÇC). Тоді всього студентів у групі 12+10+8-5-4-3+1=19.

За допомогою формули (1) можна обчислити кількість елементів деякої множини U, що не належать жодній з її підмножин A1, A2, …, An:

|U(A1ÈA2È…ÈAn)|=|U|–|A1|–|A2|–…–|An|+|A1ÇA2|+|A1ÇA3|+…+
+|An-1 ÇAn|–|A1ÇA2ÇA3|–…–|An-2ÇAn-1ÈAn|+…+(-1)n|A1ÇA2Ç…ÇAn|. (2)

Формулу (2) також називають формулою включень і виключень.

7. Біноміальні коефіцієнти

Означення. Біном Ньютона – це вираз вигляду (a+b)n.

Біном розкладається в суму одночленів, які є добутками деяких степенів його доданків a і b. Школярі-восьмикласники знають формули розкладу бінома Ньютона в многочлен із степенями a і b при n=2 та 3:

(a+b)2=a2+2ab+b2,

(a+b)3=a3+3a2b+3ab2+b3.

Спробуємо розкласти (a+b)n в многочлен у загальному випадку n. Запишемо його у вигляді, пронумерувавши дужки:

1 2 … n

(a+b)(a+b)…(a+b).

Очевидно, що кожний доданок містить n множників – k множників a і n-k множників b, тобто має вигляд akbn-k, де k£n, k³0. Кожний такий доданок взаємно однозначно відповідає підмножині номерів дужок, з яких для утворення цього доданка ми брали множники a. Таким чином, доданків akbn-k рівно стільки, скільки таких підмножин, тобто =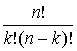. Отже,

(a+b)n =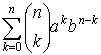

Коефіцієнти при akbn-k називаються біноміальними, оскільки записуються в розкладі бінома (a+b)n.

Біноміальні коефіцієнти мають очевидну властивість симетрії:

= =..

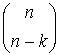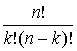Розглянемо окремі випадки бінома Ньютона:

при b=1 маємо (a+1)n = ,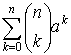

при a=b=1 маємо (1+1)n = 2n = ,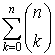

при a= –1, b=1 маємо (–1+1)n = 0n = 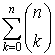(–1)k.

За останньою рівністю, зокрема, природно означити 00 як 1, слідуючи за Доналдом Кнутом [****].

Запишемо біноміальні коефіцієнти для початкових значень n=0, 1, …, 5 у трикутну таблицю:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

З таблиці видно, що кожний елемент, який не є першим у своєму рядку, є сумою елемента над ним і елемента, розташованого над ним і ліворуч:

= +

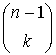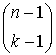
Ця тотожність називається правилом додавання. Існує багато різних її доведень. Ось "лобове":

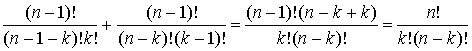
Доозначимо біноміальні коефіцієнти при k<0 та k>n як =0. Тоді правило додавання справджується за будь-яких значень k. Скористаємося цим доозначенням також і далі, розглядаючи суми, в яких додавання ведеться за нижнім коефіцієнтом k у виразах вигляду . Це дозволить не записувати межі, у яких змінюється k.

Доведемо ще одну тотожність, яка називається згорткою Вандермонда:

.

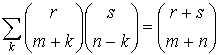Якщо замінити k на k-m, а n – на n-m, то одержимо рівність

.

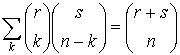Вона має назву тотожності Коші. Доведемо спочатку цю рівність. Нехай є r дівчат і s юнаків. Праворуч маємо кількість способів вибрати з них усіх n осіб. Кожний доданок у сумі ліворуч задає кількість способів вибрати n осіб так, щоб серед них було k дівчат з r і n-k юнаків з s. Додавання цих кількостей по всіх можливих значеннях k дає кількість всіх способів вибрати з них усіх n осіб. Отже, вирази ліворуч і праворуч задають одну й ту саму кількість, тобто рівні. Якщо тепер замінити назад k на k+m, а n на n+m, одержимо початкову рівність.

Таблиця біноміальних коефіцієнтів зображається ще у вигляді так званого арифметичного трикутника, або трикутника Паскаля:

1

1 1

1 2 1

1 3 3 1

…

Розширимо поняття біноміальних коефіцієнтів на дійсні значення n. Згадаємо зв'язок між кількістю комбінацій з n елементів по k та кількістю їх розміщень без повторень: = (n)k/k!, де (n)k=n(n–1)…(n–k+1). Але останній добуток означений при будь-якому дійсному значенні n. Слідуючи Доналду Кнуту [****], замість цілого n розглянемо дійсне r: (r)k=r(r–1)…(r–k+1). Тоді за дійсних значень r означимо як (r)k/k!.