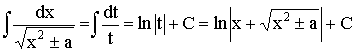Реферат: Метод безпосереднього інтегрування

Цей метод базується на рівності , де а та b – де сталі і застосовується у тих випадках, коли підінтегральна функція f має вигляд однієї із підінтегральних функцій таб­личних інтегралів, але її аргумент відрізняється від змінної інтегрування постійним доданком або постійним множником або постійним множником та постійним доданком.

Приклад 3. Знайти інтеграли

Розв’язування.

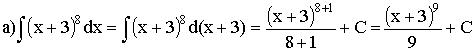
У цьому випадку змінна інтегрування х відрізняється від аргументу степеневої функції u8 = (х + 3)8 на постійний доданок 3;

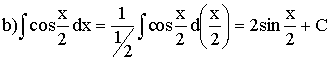
У цьому випадку аргумент функції косинус відрізняється від змінної інтегрування х на множник ½.

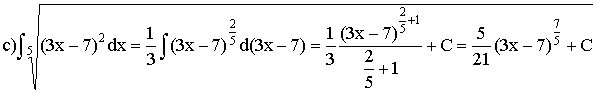
У цьому випадку змінна інтегрування х відрізняється від аргу­мента степеневої функції u2/5 = (3х - 7)2/5 постійним множником 3 та постійним доданком (- 7).

Метод підстановки (заміни змінної)

Цей метод містить два прийоми.

а) Якщо для знаходження заданого інтеграла зробити підстановку х = (t), тоді має місце рівність

Після знаходження останнього інтеграла треба повернутись до початкової змінної інтегрування х. Для застосування цього прийому треба, щоб функція х = (t) мала обернену t = (х).

Приклад 4. Знайти інтеграл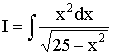

Розв’язування. Зробимо підстановку x = 5sin t, тоді

Отже, одержимо

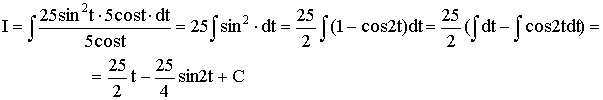
Із рівності х = 5 sin t одержимо t = arcsin (x/5);

Отже,

b) Якщо зробити заміну змінної, тобто t = (х) тоді має місце рівність .

Після знаходження останнього інтеграла треба по вернутись до змінної х, використовуючи рівність t = (х).

Зауваження:

Якщо підстановка обрана вдало, то одержаний інтеграл буде простішим і мета підстановки досягнута.

Якщо підінтегральний вираз містить корень вигляду , то доцільно застосувати тригонометричну підстановку х = a cos t або х = а sin t

Знаходження вдалої підстановки для інтегрування певної множини функцій є значною подією в інтегральному численні. Видатний вчений XVIII віку, член Петербурзької академії наук Л.Ейлер вказав підстановку для знаходження інтеграла 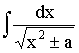. У цьому випадку

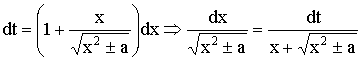або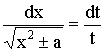

Отже,