Реферат: Критерій інтегрованості функцій

Комбінацією, що інтегрується, називається диференціальне рівняння, отримане шляхом перетворень із системи, диференціальних рівнянь, але яке вже можна легко інтегрувати.

.

Одна комбінація, що інтегрується, дає можливість одержати одне кінцеве рівняння

,

яке є першим інтегралом системи.

Геометрично перший інтеграл являє собою -вимірну поверхню в -вимірному просторі, що цілком складається з інтегральних кривих

Якщо знайдено -комбінацій, що інтегруються, то одержуємо перших інтегралів

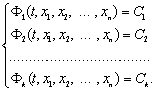
І, якщо інтеграли незалежні, то хоча б один з визначників . Звідси з системи можна виразити - невідомих функцій через інші і підставивши їх у вихідну систему, понизити порядок до - рівнянь. Якщо і всі інтеграли незалежні, то одержимо загальний інтеграл системи.

Особливо поширеним засобом знаходження комбінацій, що інтегруються, є використання систем у симетричному вигляді.

Систему диференціальних рівнянь, що записана в нормальній формі

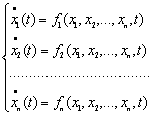
можна переписати у вигляді

..

При такій формі запису всі змінні рівнозначні.

Система диференціальних рівнянь, що записана у вигляді

,

називається системою у симетричному вигляді.

При знаходженні комбінацій, що інтегруються, найбільш часто використовується властивість “пропорційності”. А саме, для систем в симетричному вигляді справедлива рівність

.

Розглянемо деякі типи диференціальних рівнянь, що інтегруються в квадратурах.

1) Рівняння вигляду

.

Проінтегрувавши його -раз одержимо загальний розв’язок у вигляді

.

Якщо задані умови Коші

,

то розв’язок має вигляд

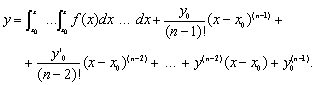
2) Рівняння вигляду

.

Нехай це рівняння вдалося записати в параметричному вигляді

Використовуючи основне співвідношення , одержимо

.

Проінтегрувавши його, маємо

.

І одержимо параметричний запис рівняння -порядку

Проробивши зазначений процес ще -раз, одержимо загальний розв’язок рівняння в параметричному вигляді

3) Рівняння вигляду

.

Нехай це рівняння вдалося записати в параметричному вигляді

Використовуючи основне співвідношення , одержуємо

. Проінтегрувавши, маємо

.

І одержали параметричний запис рівняння -порядку

Використовуючи попередній пункт, понизивши порядок на одиницю, запишемо

Проробивши останню процедуру -раз, запишемо загальний розв’язок у параметричному вигляді

4) Нехай рівняння вигляду

можна розв'язати відносно старшої похідної

.

Домножимо його на й одержимо

.

Перепишемо його у вигляді

.

Проінтегрувавши, маємо

,

тобто ,

або

.

Таким чином одержали параметричний запис рівняння -порядку

і повернулися до третього випадку.