Реферат: Інваріантність

Задача 2.

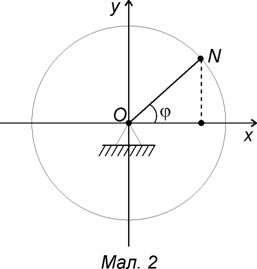
Кривошип ON довжиною a обертається навколо вісі, перпендикулярної до площини малюнка 2 і яка проходить через точку О. Кут між нерухомою віссю Ох і кривошипом змінюється пропорційно до часу: . Скласти рівняння руху точки N в декартовій системі. Визначити рівняння її траєкторії. Визначити час одного повного оберту точки N в момент часу коли обидві координати точки рівні між собою.

Розв’язок: Для складання рівняння руху точки N потрібно виразити її координати як функції часу. З малюнку заходимо координати і точки : ; або . Це і буде шуканим рівнянням руху точки . Щоб знайти рівняння траекторії в аналітичній (явній) формі треба виключити із і

Тобто траекторія точки представлятиме собою коло радіуса з центром в початку координат.

Визначимо час одного повного оберту точки . Це є час , протягом якого кут зміниться на радіан.

, звідки

Для знаходження початкового положення точки необхідно в рівнянні руху підставити значення . Тоді .

Визначимо момент часу, коли обидві координати точки рівні між собою і , тобто , звідки , де . А це значить, що моменти часу, координати точки рівні між собою будуть

Задача 3.

Циліндричні координати точки при її русі відносно деякої системи відліку змінюються по закону: .