Реферат: Інтегрування ірраціональних виразів

План

Інтегрування деяких ірраціональних функцій

Інтеграли від виразів

Підстановки Чебишева

1. Інтегрування деяких ірраціональних функцій

У цьому пункті раціональні функції однієї змінної, наприклад , двох змінних, наприклад і , трьох змінних далі позначатимемо так:

Істинними є такі твердження:

а) Усі функції, що можуть бути зведені до вигляду де ціле число, довільні дійсні числа, інтегруються в замкненому вигляді (тут взято за , а роль відіграє ). Доведення пропонується здійснити самостійно, скориставшись підстановкою . Пропонується також, як приклад, проінтегрувати функцію .

б) Усі функції, що можуть бути зведені до вигляду , якщо , інтегруються в замкненому вигляді за допомогою заміни змінної . Пропонується самостійно переконатися в цьому, а також розглянути випадок .

Рекомендується практично переконатися в цьому на прикладі

інтегрування функції .

в) Інтеграл 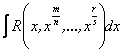зводиться до інтеграла від раціональної функції за допомогою підстановки де

спільний знаменник дробів

г) Інтеграл 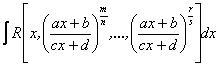зводиться до інтеграла від раціональної функції за допомогою підстановки

де спільний знаменник дробів

д) Усі функції, що можуть бути зведені до вигляду , інтегруються в замкненому вигляді. Розглянемо тут можливі випадки за умови, звичайно, що .

За допомогою підстановок (їх уперше застосував Л.Ейлер)

(8.25)

заданий інтеграл зводиться до інтеграла від раціонального дробу, а це означає , що заданий інтеграл подається через елементарні функції, тобто інтегрується в замкненому вигляді.

Пропонується довести це твердження і проілюструвати таку можливість на прикладах:

Цього самого типу інтеграли можна проінтегрувати й інакше.

Маємо . Якщо то останній вираз матиме вигляд де . Якщо тепер здійснити заміну змінної (у випадку верхнього знака) або (у випадку нижнього знака) , то заданий інтеграл зведеться до інтеграла від раціональної функції відносно і . При .

Якщо , матимемо тобто одержимо функцію від комплексної змінної, яка тут не розглядається. Якщо при , то , тобто підстановка (або ) зведе заданий інтеграл до інтеграла від раціональної функції відносно і,

де .Отже, в усіх випадках, за яких , інтеграл зводиться до інтеграла вигляду , який детально розглядатимемо далі.

е) Усі функції вигляду інтегруються у замкненому вигляді за допомогою заміни змінної і зводяться до інтеграла з , який розглянуто в попередньому пункті. Пропонується цей факт довести самостійно і, як приклад, проінтегрувати функцію

.

є) Інтеграл від біноміального диференціала обчислюються за допомогою однієї із підстановок:

1. Якщо ціле, то де спільний знаменник дробів і

2. Якщо ціле, де знаменник

3. Якщо ціле, то де знаменник

Російським математиком П. Л. Чебишевим доведено, що інших випадків інтегровності в замкненому вигляді біноміальних диференціалів не існує. Ці три підстановки називають підстановками Чебишева.