Реферат: Інтегрування деяких рівнянь другого порядку шляхом пониження порядку рівняння

Перепишемо це рівняння таким чином

Оскільки розв’язки однорідного рівняння, то вирази в дужках тотожньо рівні нулю; тому із останнього рівняння одержимо

Отже, ми одержали систему рівнянь для визначення похідних аналогічну системі (12.36)

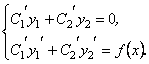(12.36а)

Із системи (12.36а) знаходимо Нехай Тоді, після інтегрування одержимо

Загальний розв’язок неоднорідного рівняння запишеться у вигляді

(12.37)

Приклад. 3. Знайти загальний розв’язок диференціального рівняння методом варіації довільних сталих.

Р о з в ‘ я з о к. Розв’яжемо відповідне однорідне рівняння

Характеристичне рівняння має корені Тоді

загальний розв’язок ЛОДР

Частинний розв’язок неоднорідного рівняння шукаємо у вигляді

де визначаються із системи (12.36а)

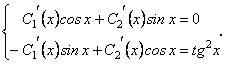
Тоді

Отже

і загальний розв’язок початкового диференціального рівняння матиме вигляд