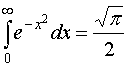Реферат: Інтеграл Ейлера

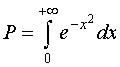
(1)

 

Функція досягає свого найбільшого значення 1 при t = 0.

Отже,

при t > 0 і t < 0.

Беручи t = ±х2, дістаємо:

звідки

(2)

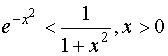(3)

Підносячи вирази (63) і (64) до степеня з будь-яким натураль­ним показником n, маємо:

(4)

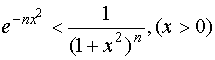(5)

Інтегруючи нерівність (65) на проміжку від 0 до 1, а нерівність (6) — від 0 до +, дістаємо:

.

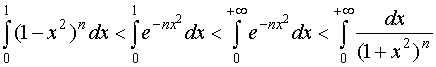Водночас виконуються такі співвідношення:

1) ;

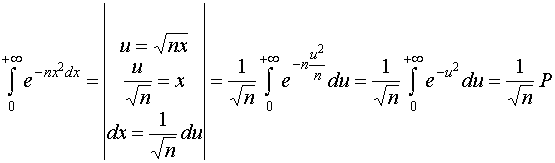2) ;

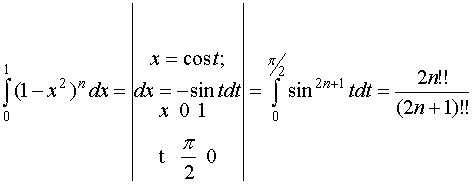3) .

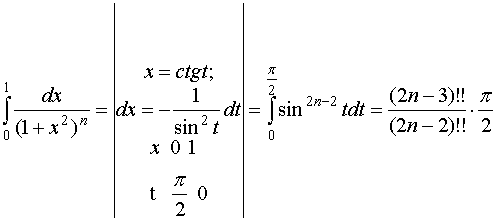Звідси

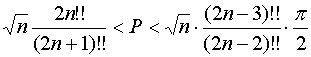
Підносячи до квадрата і перетворюючи вираз (67), дістаємо:

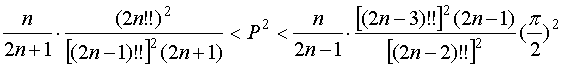.(7)

Із формули Вілліса

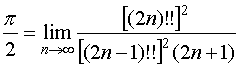
випливає, що обидва крайні вирази у (68) при п — прямують до , тому

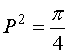і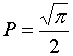

Отже,