Реферат: Функція Гріна
Нехай в банаховому просторі Z визначена крайова задача
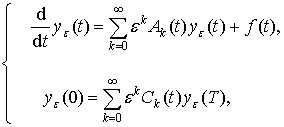(1)
де
для довільного 
і 
являються лінійними обмеженими операторами, які діють в Z,
ряди в правих частинах (1) збігаються у рівномірної операторної топології при , 
, 
, 
,
, 
, сильно неперервні при ,
,
оператор 
, де 
- оператор Коші однорідного рівняння
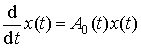, (2)
є 
- оператор [1] з 
Лема. Якщо власна функція 
крайової задачі
, 
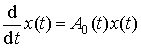, (3)
відносно операторів і 
, утворює узагальнений Жорданов ланцюг приєднаних функцій 
, скінченої довжини 
, то для достатньо малих 
крайова задача (1) має єдиний розв’язок.
Теорема. Якщо виконуються умови леми, то для крайової задачі (1) існує функція Гріна 
і для неї має місто лорановський розклад
,
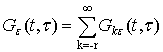де
де
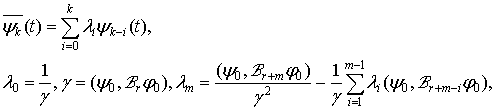
- власна функція крайової задачі, спряженої до задачі (3); 
- узагальнений жорданів ланцюг, відносно операторів 
,спряжений до ланцюга 
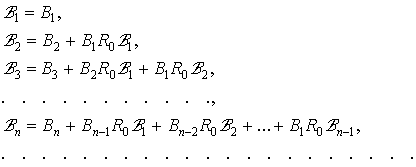
- узагальнено обернений до 
;
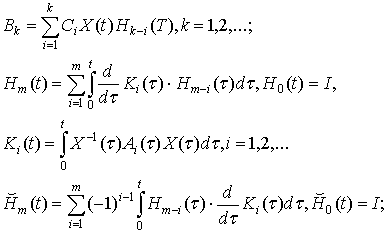
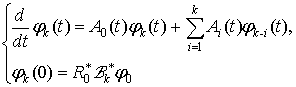
- розв’язки задач Коші
- розв’язки задач Коші
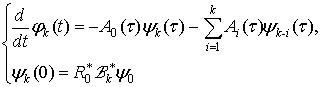
Використана література
М.М. Вайнберг, В.А. Треногин Теория ветвления решений нелинейных уравнений «Наука», М., 1969., 527с.